1Nel giardino di Matteo vi sono 8 buche. Il giardiniere copre metà di ciascuna buca con delle pietre. Quante sono le buche in quel giardino dopo il lavoro del giardiniere?

2Quanti sono, in un anno solare, i mesi che contengono il giorno 30?

3Vi sono 8 canguri nelle caselle della figura a destra. Trova il minimo numero di canguri a cui ti basta far cambiare casella se vuoi che ogni riga e ogni colonna della tabella contenga esattamente 2 canguri.

4Daniele vuole riempire una vasca d’acqua per la sua tartaruga. La vasca si riempie con il contenuto di 4 secchi. Daniele riempie il secchio ad una fontana ma, ad ogni viaggio che fa dalla fontana alla vasca con il secchio colmo, perde metà del contenuto. Qual è il minimo numero di viaggi, dalla fontana alla vasca, che permetterà a Daniele di riempire la vasca?

5In un circo, dopo il primo colpo di frusta del domatore, le tigri si dispongono su 3 file: in ogni fila vi sono esattamente 4 tigri. Il domatore vuole che, al secondo colpo di frusta, le tigri si dispongano in file complete di 5 tigri ciascuna e che rimangano in scena quante più tigri possibile. Quante tigri dovranno abbandonare la scena?

6Ogni figlio (maschio o femmina) dei signori Rossi ha almeno un fratello e una sorella e il numero dei figli dei signori Rossi è il più piccolo che consente il verificarsi di questa circostanza. Quanti figli hanno i signori Rossi?

7Elisabetta aveva una tavoletta rettangolare di cioccolato formata da quadratini di 1 cm x 1 cm. Ha mangiato alcuni di questi quadratini ed il pezzo di cioccolato che rimane ha la forma in figura. Quanti quadratini restano ancora?

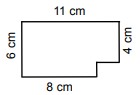
8Rileggi il quesito precedente: “Elisabetta aveva una tavoletta rettangolare di cioccolato formata da quadratini di 1 cm x 1 cm. Ha mangiato alcuni di questi quadratini ed il pezzo di cioccolato che rimane ha la forma in figura.” Ora ti chiediamo: quanti quadratini di cioccolato ha mangiato Elisabetta?

9Due segnali stradali si trovano all’imboccatura di un ponte. Essi indicano la massima larghezza, 325 cm, ed il massimo peso, 4300 kg, consentiti per un veicolo che debba attraversare quel ponte. Quale dei seguenti automezzi è autorizzato ad attraversare quel ponte?

10Tra i 5 numeri elencati qui sotto, quello che ho scelto è pari; tutte le cifre che lo formano sono diverse fra loro; la cifra delle centinaia è doppia di quella delle unità; la cifra delle decine è maggiore della cifra delle centinaia. Che numero ho scelto?

11Su un foglio di carta è disegnato un rettangolo di dimensioni 17 cm x 13 cm che voglio suddividere in quadrati di 1 cm di lato. Dispongo di un righello lungo 20 cm. Qual è il minimo numero di segmenti che mi basta tracciare per raggiungere lo scopo?

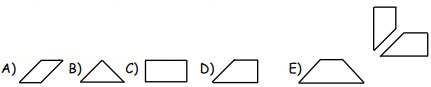
12Un foglio di carta quadrato è stato tagliato in tre parti. Due di queste sono rappresentate a destra. Quale delle seguenti può essere la terza?

13Vi erano 15 pezzi di carta. Dopo che alcuni sono stati tagliati in 3 parti, i pezzi di carta sono diventati 23. Quanti pezzi di carta sono stati tagliati?

14Tre uomini, lontani uno dall’altro, camminano lungo un viale dotato, ad intervalli regolari, di panchine numerate. In uno stesso momento tutti e tre si siedono per riposare. Il primo uomo si siede sulla panchina numero 66, il terzo uomo sulla panchina numero 24 e il secondo uomo a metà strada tra i due. Qual è il numero della panchina su cui si siede il secondo uomo?

15Pietro ruota un triangolo in senso orario di una posizione al secondo (osserva la figura, dove sono rappresentate nell’ordine la posizione iniziale P, quella dopo 1 secondo e quella dopo 2 secondi). Quale sarà la posizione del triangolo dopo 2005 secondi?

16In casa vi sono due gatti, Tiny e Tony, e due cani, Dim e Dill. Tiny ha paura di entrambi i cani mentre Tony ha paura di Dim, ma non di Dill. Quale affermazione (riferita a questi gatti e a questi cani) è falsa?

17La portata massima di un ascensore è 150 chili. Quattro amici devono usarlo per raggiungere dal piano terra il decimo piano: tre di essi pesano 80 chili ciascuno, mentre il quarto pesa 60 chili. Qual è il minimo numero di viaggi in salita dell’ascensore che consente di portare al piano desiderato i quattro amici?

18Esiste un solo rettangolo che puoi realizzare utilizzando 6 fiammiferi, quello illustrato in figura. Quanti rettangoli differenti per dimensioni puoi comporre utilizzando (per ognuno) 14 fiammiferi? (Tutti i fiammiferi hanno la stessa lunghezza.)

19Edoardo, Susanna e Teresa giocano a carte. Al termine di ogni partita, il vincitore guadagna 3 punti, il secondo classificato 1 punto mentre il terzo classificato non guadagna punti. Dopo quattro partite, Susanna ha 4 punti e Teresa 3. Quante partite ha vinto Edoardo?

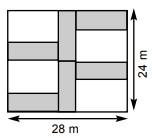
20La figura a lato mostra un giardino rettangolare di dimensioni 24 metri per 28 metri. Il giardiniere ha realizzato sei aiuole rettangolari di identiche dimensioni (colorate in grigio nella figura). Qual è il perimetro di ogni aiuola?

21Libor ha scelto due numeri interi maggiori di zero, uno di tre cifre e uno di due cifre. La loro differenza è 989. Quanto vale la loro somma?

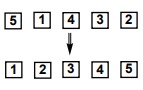
22Cinque carte, numerate da 1 a 5, sono allineate sul tavolo nell’ordine 5, 1, 4, 3, 2. Devi mettere le carte nell’ordine 1, 2, 3, 4, 5 eseguendo solo mosse del seguente tipo: ogni mossa consiste nello scambiare fra loro due carte. Qual è il minimo numero di mosse che ti consente di realizzare l’operazione?

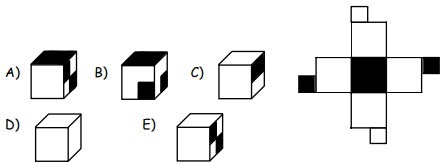
23Uno solo dei seguenti cubi ammette lo sviluppo presentato a destra. Quale?

24Il prodotto di 100 numeri interi maggiori di zero è uguale a 100. Qual è il minimo valore che può avere la somma di questi numeri?