1Ieri è stato il compleanno di Matteo. Domani sarà giovedì. In quale giorno della settimana è caduto il compleanno di Matteo?

2Abbiamo a disposizione diversi tavoli quadrati uguali: per la festa della scuola ne abbiamo accostati 7, formando un lungo tavolo rettangolare. Se ad ogni tavolo quadrato possono sedere quattro persone, una per ogni lato, qual è il massimo numero di persone che possono sedere intorno al tavolo rettangolare?

3Sotto puoi vedere le monete che hai nel borsellino. Un lecca lecca costa 10 centesimi. In quanti modi differenti puoi comporre l'importo con cui pagarlo? (Considera non distinguibili due monete di uguale valore.)

4Nel disegno di sotto sono rappresentati nove gettoni disposti a triangolo. Vuoi realizzare un quadrato: qual è il minimo numero di gettoni che ti basta spostare?

5Il postino Gennaro ha due timbri che può usare indifferentemente: uno a forma di quadrato e l'altro di triangolo. Deve annullare i francobolli posti su dieci buste usando un solo timbro per ogni busta. Quanti timbri triangolari può apporre al massimo, se vuole che, comunque prese tre di quelle buste, una almeno non abbia il timbro triangolare?

6Tra due punti sono state disegnate le quattro strade che ti proponiamo. Quale fra esse è la più corta?

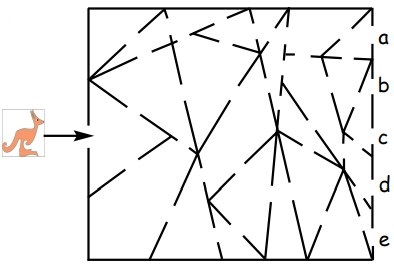
7Un canguro entra nell'edificio di cui vediamo la pianta di sotto. Se vuole attraversare esclusivamente stanze di forma triangolare, dovrà uscire dall'edificio dalla porta

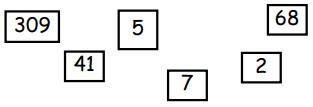
8Osserva la figura: sei numeri sono scritti su altrettanti foglietti. Accostando tutti i sei foglietti puoi formare dei numeri di dieci cifre. Qual è il più piccolo?

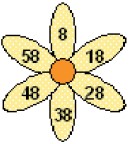
9Nella figura a lato puoi vedere un fiore numerato. Maria stacca tutti i petali con numeri che, divisi per 6, danno resto 2. Quanto vale la somma dei numeri sui petali che Maria ha staccato?

10Pietro ha esattamente un fratello e sua sorella Caterina ha tanti fratelli quante sorelle. Quanti sono i figli (maschi e femmine) nella famiglia di Pietro?

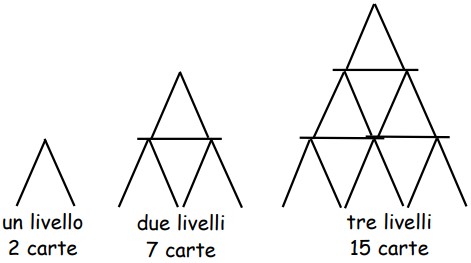
11Stefania sta costruendo castelli di carte. Nella figura si possono osservare i castelli di uno, due e tre livelli che ha finora costruito. Quante carte dovrà usare Stefania per costruire un intero castello di 4 livelli?

12Uno scoiattolo inizia a mangiare noccioline. Ne mangia una e, durante ogni minuto successivo, mangia una nocciolina in più di quelle mangiate nel minuto precedente. Quanti minuti impiegherà per mangiare 78 noccioline?

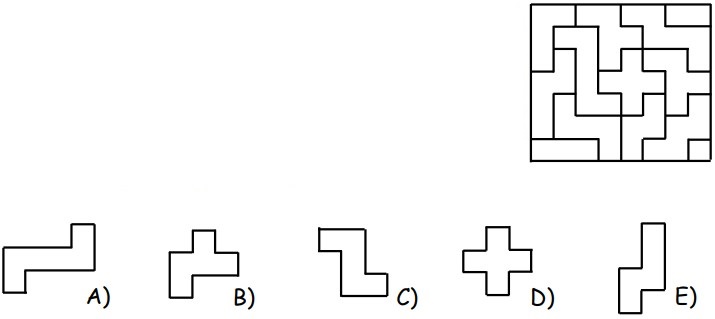
13In figura è rappresentato un puzzle ottenuto accostando varie tessere; alcune di esse hanno la forma di quattro delle cinque figure rappresentate qui sotto. Rispetto alle figure rappresentate, le tessere possono essere eventualmente ruotate o trascinate, ma non ribaltate. Quale figura non è stata usata per comporre il puzzle?

14Sei pesi da 1, 2, 3, 4, 5 e 6 grammi sono stati chiusi in tre scatole vuote, due pesi per ogni scatola. Il contenuto della prima scatola pesa 9 grammi, quello della seconda pesa 8 grammi. Quali pesi sono stati inseriti nella terza scatola?

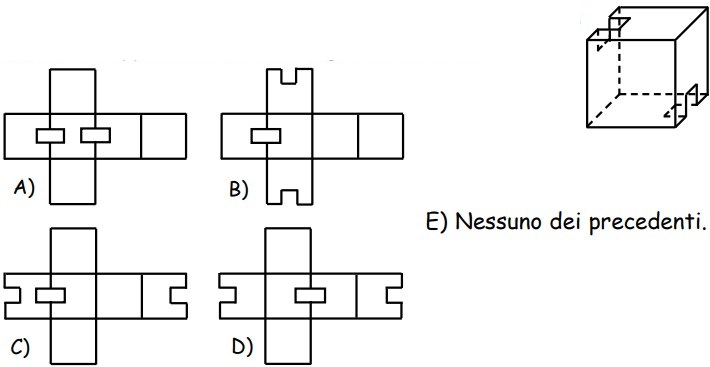
15Qual è lo sviluppo piano della superficie cubica con due buchi rappresentata nella figura a destra?

16Quattro corvi sono appollaiati su una trave. I loro nomi sono Ala, Blu, Cra e Dan. Ala è appollaiata esattamente a metà tra Blu e Cra. La distanza tra Blu e Ala è uguale a quella tra Cra e Dan. Ala dista 4 metri da Dan. Quale distanza intercorre tra Blu e Dan?

17La scrittura 81x7 = 623 descrive un'operazione errata. Si può però rimediare all'errore cambiando una cifra sola: quale?

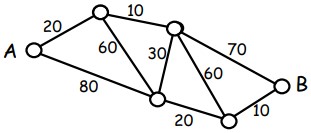
18I piccoli cerchi in figura rappresentano altrettante città. Ogni segmento che congiunge due cerchi rappresenta una linea ferroviaria che unisce le corrispondenti città ed il numero più vicino ad esso indica il costo in euro del biglietto per quella tratta. Paolo ha organizzato il viaggio per andare da A a B spendendo il meno possibile. Quanto ha speso?

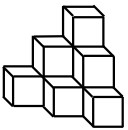
19La struttura mostrata in figura è formata da 10 cubi incollati fra loro. Romano dipinge l'intera struttura, incluso il fondo. Quante facce di cubi sono state verniciate?

20Irene, Anna, Clara, Olga ed Elena vivono nello stesso edificio: di esse, due abitano al primo piano, le altre al secondo piano. Olga abita su un piano diverso rispetto a Clara ed Elena. Anna abita su un piano diverso rispetto a Irene e Clara. Chi abita al primo piano?

21Nella scrittura 2002 * 2003 * 2004 * 2005 * 2006 immagina di sostituire ogni simbolo * con un + o un - (non necessariamente sempre lo stesso segno): a seconda delle scelte operate sono possibili tanti risultati diversi. Uno solo dei seguenti risultati è impossibile ottenere: quale?

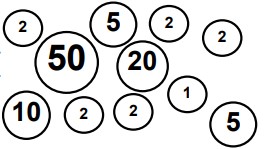
22Ho scritto tutti i numeri interi di quattro cifre su altrettanti foglietti verdi (un numero per ogni foglietto). Poi ho scritto tutti i numeri interi di una cifra su altrettanti foglietti gialli (un numero per ogni foglietto). In quanti modi posso scegliere due foglietti di colore diverso, se voglio che la differenza dei due numeri scritti su di essi sia un numero di 3 cifre?

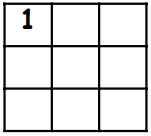
23In ognuna delle nove celle della griglia quadrata in figura vogliamo inserire una delle cifre 1, 2 o 3. La sola condizione è che ciascuna cifra compaia in ogni riga e in ogni colonna. Nella cella in alto a sinistra abbiamo già inserito la cifra 1. In quanti modi diversi possiamo completare la griglia?

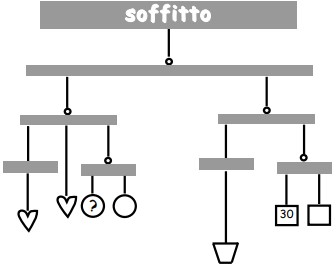
24Miriam ha appeso al soffitto della sua stanza il gioco mobile che vedi in figura. Barre e pendagli di ugual forma hanno lo stesso peso e tutta la struttura è in perfetto equilibrio. Ogni pendaglio quadrato pesa 30 grammi. Qual è il peso di ogni pendaglio circolare?