1Esegui nell’ordine le operazioni indicate sopra ogni freccia. Che numero va scritto nell’ultima nuvoletta?

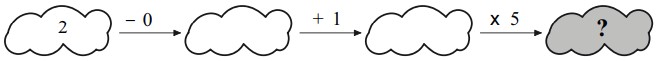
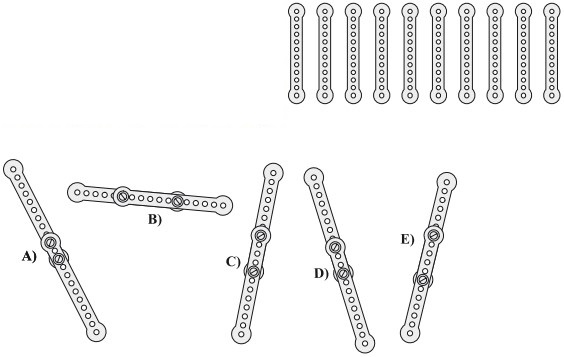
2Enrico ha le 10 barre di metallo tutte uguali che vedi in figura. Con delle viti le unisce a coppie per formare le 5 barre più lunghe che sono mostrate nelle figure che costituiscono le risposte. Qual è la più lunga di tutte?

3La figura mostra due addizioni, ma due dei quattro addendi sono coperti ciascuno da un triangolo e un terzo addendo è coperto da un quadrato. I due numeri coperti dai due triangoli sono uguali fra loro. Qual è il numero coperto dal quadrato?

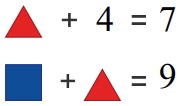
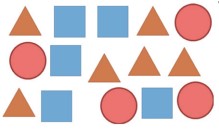
4Sul tavolo vi sono diversi foglietti. Alcuni sono a forma di cerchio, altri di quadrato, altri ancora di triangolo, come mostra la figura. Se vuoi che sul tavolo rimangano solo foglietti tutti della stessa forma, qual è il più piccolo numero di foglietti che ti basta levare?

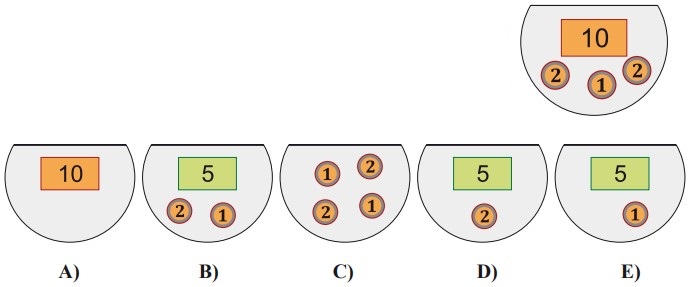
5La figura mostra il denaro che Lucia aveva nel suo borsellino prima di entrare in un negozio, dove ha speso 7 euro: un biglietto da 10 euro, due monete da 2 euro e una moneta da 1 euro. Quale delle seguenti figure può mostrare il denaro che Lucia ha nel borsellino ora che è appena uscita dal negozio?

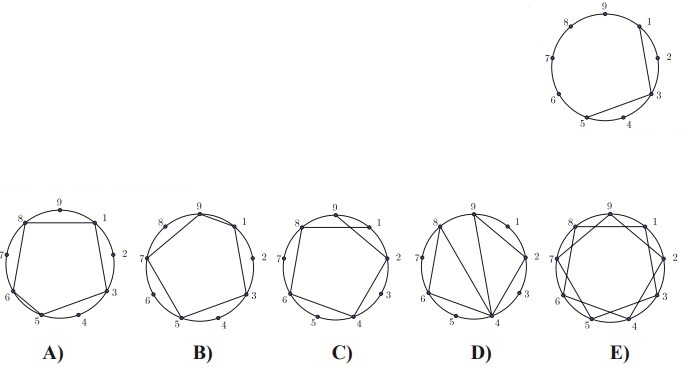
6Su una circonferenza sono segnati 9 punti e sono numerati. Partendo dal punto 1, Giacomo ha tracciato il segmento che lo unisce al punto 3, quindi ha tracciato il segmento che unisce il punto 3 al punto 5: la figura ti mostra ciò che ha fatto Giacomo fino ad ora. Ora Giacomo ha intenzione di proseguire in questo modo nel tracciare i segmenti, saltando un punto ogni volta, e fermandosi quando sarà ritornato di nuovo al punto 1. Tra i seguenti percorsi, qual è quello che Giacomo dovrà tracciare?

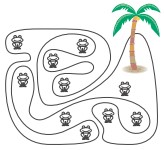
7La figura mostra un’isola molto frastagliata e 10 rane. Alcune rane stanno in acqua: quante stanno sull’isola?

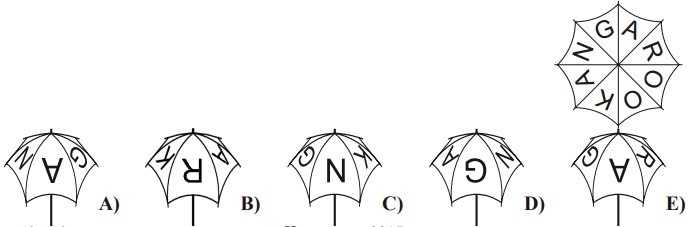
8Guardando il mio ombrello dall’alto, come mostrato nella figura a fianco, si legge la parola KANGAROO (Canguro in inglese). Quale delle figure che seguono potrebbe rappresentare il mio ombrello?

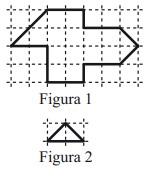
9Bruno vuole scomporre la regione determinata dal contorno scuro nella figura 1 in triangoli tutti uguali a quello che appare nella figura 2. Quanti triangoli otterrà?

10Carlo aveva 7 mele e 2 banane. Ha dato 2 mele a Gianni che, in cambio, gli ha dato alcune banane. Ora il numero delle mele e il numero delle banane che Carlo ha sono uguali. Quante sono le banane che Gianni ha dato a Carlo?

11Sara aveva molti cubetti grigi e molti cubetti bianchi. Accostandone 27 in modo che due cubetti dello stesso colore non avessero mai alcuna faccia in comune, ha costruito il cubo grande che vedi in figura. Quanti cubetti bianchi ha usato?

12In una gara cui hanno preso parte 30 concorrenti, Gennaro ha superato 3 concorrenti in più di quanti hanno superato lui. Come si è classificato Gennaro?

13Stefano ha 4 modellini: un camion, un’automobile, una nave e un treno. Li vuole mettere in fila in modo che sia la nave sia il treno vengano dopo l’automobile. In quanti modi diversi può allineare i suoi giocattoli?

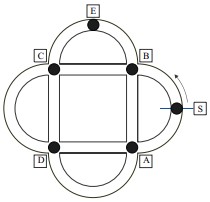
14Nel parco c’è una pista ciclabile come quella mostrata in figura, 6 punti della quale sono indicati da altrettante lettere. Pietro parte dal punto S muovendosi nella direzione indicata dalla freccia: al primo incrocio che trova gira a destra, al secondo gira a sinistra, al terzo a destra, al quarto a sinistra e così via, alternando la scelta di destra con la scelta di sinistra. Pur ripassando molte volte dal punto S, c’è un punto (e uno solo) per il quale, così facendo, Pietro non passa mai: qual è?

15La figura ti mostra cinque coccinelle: ognuna di esse ha alcuni punti neri sul dorso. Due coccinelle sono amiche se e solo se i numeri dei loro punti neri differiscono di uno. Oggi è la festa delle coccinelle: ognuna manda un messaggio di auguri a ciascuna delle sue amiche. Quanti sono in totale i messaggi inviati oggi dalle coccinelle?

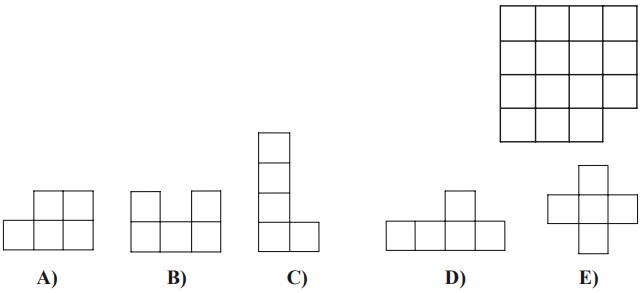
16La figura che vedi è ottenuta accostando alcuni quadratini tutti uguali. Maria è riuscita a spezzarla in tre pezzi, tutti uguali fra loro, eventualmente dopo averne ribaltato qualcuno. A quale dei seguenti sono uguali i tre pezzi?

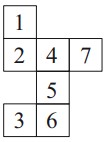
17Voglio rivestire di carta una scatola a forma di cubo, senza sovrapposizioni. Per questo ho disegnato su un foglio di carta e ritagliato la figura che vedi qui a fianco (composta da quadrati tutti uguali tra loro e uguali alle facce della scatola), che poi piegherò lungo ciascun lato comune a due quadrati. Per errore, però, ho disegnato 7 quadrati invece di 6. Devo quindi eliminarne uno, ma voglio che il foglio di carta non si spezzi in due e in particolare che non ci sia alcun quadrato unito solo per un vertice ad un altro. Qual è il numero del quadrato che va eliminato?

18In figura vedi tre fogli quadrati trasparenti: ciascuno di essi è ripartito in 9 quadratini e, su ciascuno, alcuni dei quadratini sono anneriti. I tre fogli vanno sovrapposti in modo che appaia un solo quadrato: possono essere ruotati come si vuole, ma non capovolti. Si vuole che, una volta sovrapposti, i quadratini che appaiono neri siano in numero maggiore possibile. Qual è questo numero?

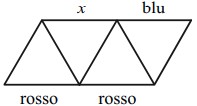
19Si deve colorare ognuno dei 9 segmenti in figura scegliendo tra i colori rosso, verde e blu e facendo in modo che, in ciascun triangolo, i 3 lati ricevano colori diversi. Come vedi, in figura sono già stati assegnati i colori a tre segmenti. Di che colore può essere il segmento segnato con x?

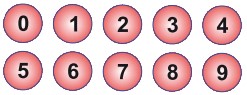
20Aldo ha dieci dischetti numerati da 0 a 9, come quelli in figura. Ne dà tre a Giovanni, quattro a Luca, tre ad Anna e chiede a ciascuno di loro di moltiplicare i numeri riportati sui dischetti che ha ricevuto: il risultato è 0 per Giovanni, 72 per Luca e 90 per Anna. Qual è la somma dei numeri riportati sui dischetti che ha ricevuto Giovanni ?

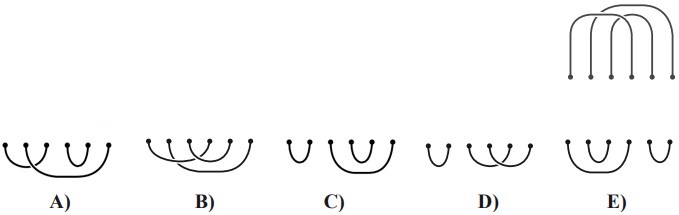
21Un anello di corda è stato gettato su un tavolo e la corda si è accavallata in alcuni punti. La corda, come giaceva sul tavolo, è stata poi tagliata in orizzontale: sopra il taglio sono rimasti i tre spezzoni di corda che vedi in figura. Di quelli indicati nelle risposte, quali possono essere i tre spezzoni rimasti sotto il taglio?

22I punti che vedi marcati in figura sono i 16 vertici di nove quadratini che, accostati, formano a loro volta un quadrato. Scegliendo di volta in volta 4 fra questi 16 punti, si possono formare vari quadrati, anche di aree diverse. Qual è il massimo numero di quadrati ottenibile, che abbiano aree tutte diverse fra loro?

23Il prodotto delle cifre di un numero intero è 15. Qual è la loro somma?

24Durante il fine settimana, sabato e domenica, cinque amici hanno cucinato dei biscotti: Anna ne ha cucinati 24, Bruno 25, Cesare 26, Davide 27 ed Elisa 28. Arrivati a domenica sera, uno di essi aveva in totale il doppio dei biscotti rispetto a quanti ne aveva cucinati sabato sera, un altro il triplo, un altro il quadruplo, un altro il quintuplo e un altro il sestuplo. Chi ne aveva cucinati di più fino a sabato sera?