1Un fungo cresce di giorno in giorno. Licia lo ha fotografato ogni giorno da lunedì a venerdì. Quale di queste sue foto è stata scattata martedì?

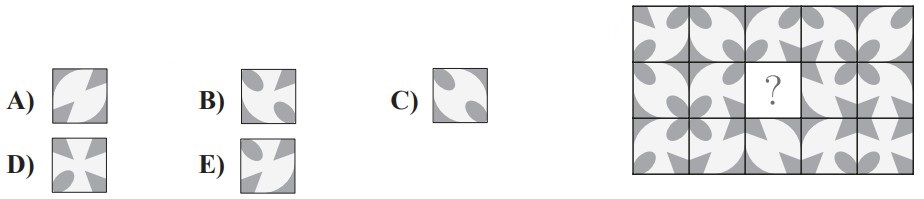
2Quale dei seguenti tasselli completa il mosaico a lato?

3In ogni cella della griglia che vedi qui a fianco è indicata un’operazione. Antonio ombreggia tutte le celle contenenti un’operazione il cui risultato è 20. Quale delle seguenti forme ottiene?

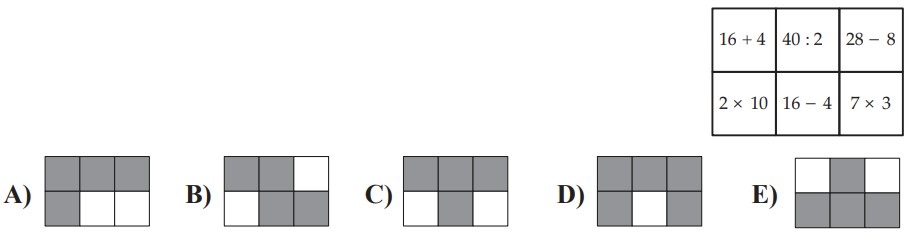
4I quadrati nelle risposte sono stati parzialmente colorati di grigio. In quale di essi la parte colorata è maggiore?

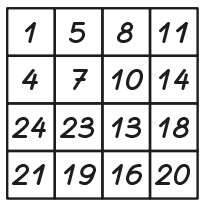
5Sonia traccia col gesso sul pavimento la grande tabella che vedi a lato, poi incomincia a saltare da una cella all’altra. Parte dalla cella numero 1 e segue questa regola: a ogni nuovo salto, atterra in una cella con un numero che è di 3 unità maggiore di quello della cella da cui ha spiccato il salto. Qual è il numero presente nell’ultima cella su cui potrà atterrare?

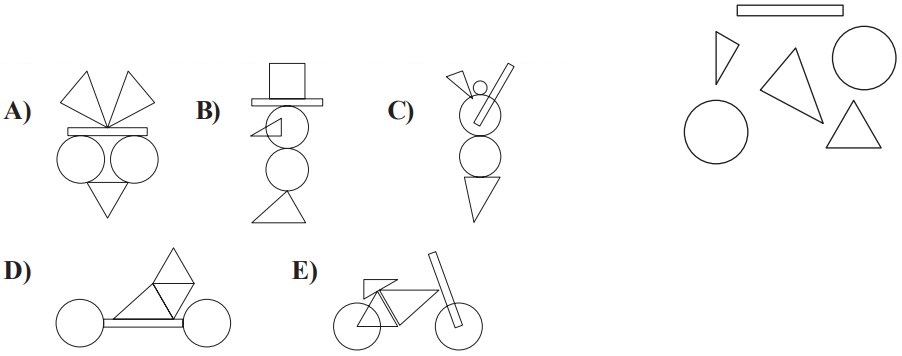
6Con i sei adesivi che vedi a lato si possono comporre diverse figure, ma una sola di quelle che vedi qui sotto. Quale?

7Giorgio incolla sei adesivi con immagini di animali, ciascuno su una faccia di un cubo. La figura qui a lato mostra il cubo in due posizioni differenti. Quale adesivo sta sulla faccia opposta a quella con l’anatroccolo?

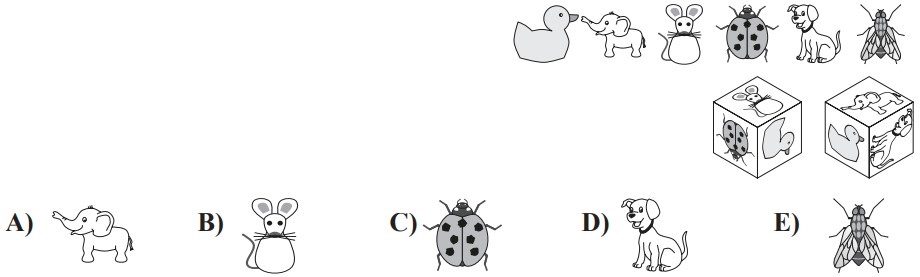
8Francesco ha le seguenti tessere. Ne userà alcune per coprire, completamente e senza sovrapposizioni, la griglia che vedi qui sotto. Se vuole usare il maggior numero possibile di tessere di misure differenti, quante tessere userà in tutto Francesco?

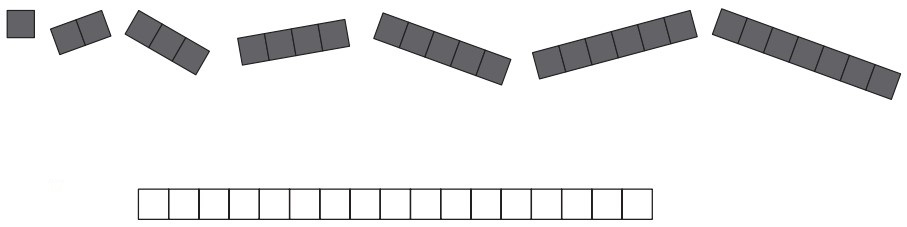
9Cinzia colora ogni regione in cui è suddiviso il cerchio che vedi sotto o di rosso o di giallo o di blu, facendo in modo che regioni che si toccano ricevano colori diversi. Cinzia colora di rosso la regione più esterna; dopo che tutto il disegno è stato colorato, quante regioni risultano colorate di rosso?

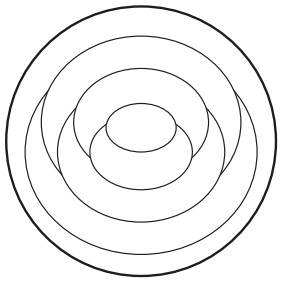
10Luca guarda dall’alto la piramide che vedi qui sotto. Quale delle immagini qui a lato vede?

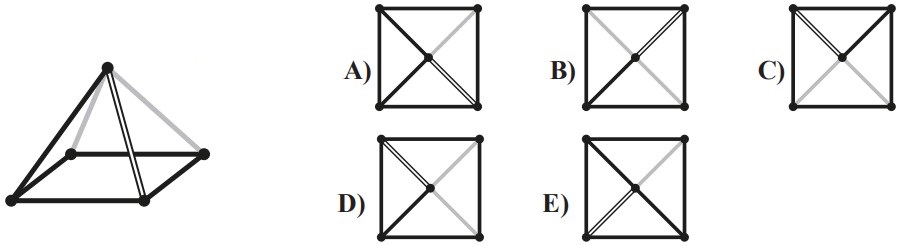
11Osserva la figura: Daniele ha legato il suo cane a un metro dall’angolo di un’edicola con pianta rettangolare i cui lati misurano 7 m e 5 m. Il guinzaglio è lungo 11 m. Ci sono 5 giochini a forma di osso nelle posizioni che vedi in figura: quanti di essi possono essere raggiunti dal cane?

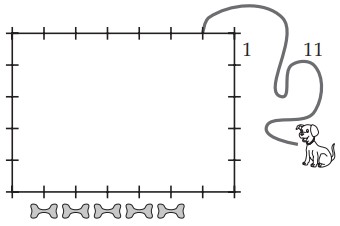
12Martino costruisce uno steccato usando pali come nella figura, ciascuno lungo un metro. In figura vedi uno steccato lungo 4 metri. Quanti pali utilizzerà Martino per costruire uno steccato lungo 10 metri?

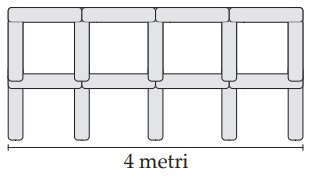
13Osserva la scala in figura: ogni volta che il coniglio scende di 3 gradini, il canguro sale di 7 gradini. Qual è il numero del gradino sul quale si incontreranno?

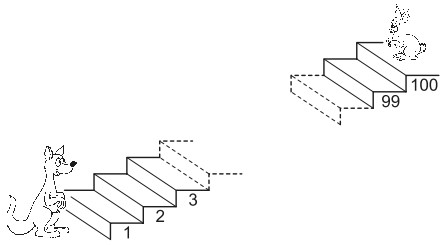
14La somma di tre numeri è 50. Cristina sottrae uno stesso numero segreto da ciascuno dei tre numeri e ottiene come risultati i numeri 24, 13 e 7. Uno solo dei seguenti è uno dei tre numeri iniziali. Quale?

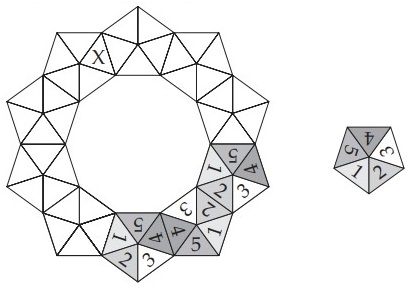
15Amalia vuol costruire una coroncina usando 10 copie del gettone che vedi a destra e vuole che quando due gettoni condividono un lato i numeri corrispondenti coincidano. Ha già disposto 3 gettoni con questo criterio. Quale numero si troverà alla fine nel triangolo denotato con X?

16Guido ha due tipi di stecchini: corti, che misurano 1 cm ciascuno, e lunghi, che misurano 3 cm ciascuno. Con quale delle combinazioni suggerite nelle risposte può costruire un quadrato, senza rompere alcuno stecchino, né sovrapporre parti di due stecchini?

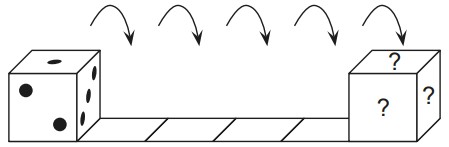
17Se osservi un dado standard vedi che, per ognuna delle tre coppie di facce opposte, il numero di puntini complessivamente presenti sulle due facce opposte è 7. Il disegno mostra un dado standard che è stato messo nella prima casella di una striscia lunga sei caselle e poi verrà fatto rotolare verso destra lungo la striscia. Quando il dado raggiungerà l’ultima casella, quale sarà il numero totale di puntini sulle tre facce indicate con punti interrogativi?

18Sei amici ordinano ciascuno una pallina di gelato. Ordinano in tutto 3 palline di vaniglia, 2 palline di cioccolato e una pallina di limone. In cima a ogni gelato c’è una decorazione scelta da una scatola contenente 3 ciliegie, 2 wafer e 1 cioccolatino e la scelta è fatta in modo che ogni gelato, una volta decorato, possa essere distinto da ciascuno degli altri. Quale delle seguenti combinazioni NON è possibile?

19Devi indovinare i nomi di tre ragazze sedute su una panchina, nell’ordine in cui sono sedute. Sai che in ognuna delle seguenti terne di nomi - Chiara, Elisa, Rosa - Chiara, Laura, Maria - Anna, Laura, Rosa - compare un solo nome corretto ed è nella posizione corretta. Quali sono nell’ordine i nomi delle tre ragazze sedute sulla panchina?

20L’insegnante ha scritto i numeri da 1 a 8 sulla lavagna, poi li ha coperti con forme geometriche: triangoli, quadrati e un cerchio. Sommando i quattro numeri coperti dai triangoli otterresti 10, sommando i tre numeri coperti dai quadrati otterresti 20; qual è il numero coperto dal cerchio?

21Gianna ha alcune immagini di pappagalli. Vuole colorare solo la testa, la coda e le ali di ogni pappagallo di rosso, blu o verde in modo che su ogni pappagallo appaiano tutti e tre i colori. Colora la testa di un pappagallo di rosso, le ali di verde e la coda di blu. Quanti altri pappagalli può colorare in modo che siano tutti colorati diversamente?

22Alcune squadre partecipano ad un campo estivo Kangourou. Ogni squadra è formata da 5 o 6 membri e in tutto ci sono 43 persone. Quante squadre ci sono nel campo?

23Quale delle seguenti “chiavi” non può essere tagliata in tre pezzi tutti diversi tra loro composti ciascuno da cinque quadratini grigi?

24Anna rimpiazza le lettere nell’espressione KAN – ROO + GA con cifre scelte tra quelle da 1 a 9: lettere uguali con cifre uguali, lettere diverse con cifre diverse. Poi calcola il risultato. Qual è il massimo risultato che può ottenere?