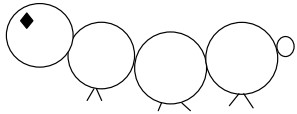1In una classe vi sono 29 studenti, le ragazze sono 3 in più dei ragazzi. Quante sono le ragazze?

2Nella giacca di un gigante vi sono 585 tasche, in ogni tasca vivono 3 topi, ed ogni topo è accompagnato da 5 topolini. Quanti topolini vivono in quella giacca del gigante?

3La somma di 5 numeri consecutivi è uguale a 2000. Il maggiore di questi numeri è:

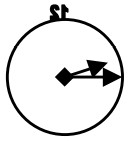
4In uno specchio vedete un orologio, quello della figura, che ore sono?

5L'anno 2000: il numero 2000 si ottiene moltiplicando unicamente dei due e dei cinque. Quanti ne servono di ogni tipo?

6Su una striscia di carta lunga 1 m disegniamo delle righe verticali che dividono la striscia in 4 parti uguali e inoltre tracciamo anche le righe, sempre verticali, che dividono la stessa striscia in 3 parti uguali. Fatto questo, tagliamo la striscia secondo le linee che abbiamo tracciato. Quante lunghezze differenti avranno i pezzi così ottenuti ?

7La somma di 7 numeri dispari consecutivi è 119. Il minore di questi numeri è

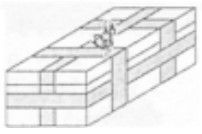
8La scatola del regalo per il compleanno di Baby Roo, il figlio di Kanga Roo, ha dimensioni 10 cm × 10 cm × 30 cm ed è stata legata con una fettuccia dorata come in figura. Qual è la lunghezza della fettuccia? La lunghezza della fettuccia per il nodo può considerarsi trascurabile.

9Charlie affitta la sua fiammante bicicletta agli amici nel modo seguente: per due tavolette di cioccolato quattro ore e per 12 caramelle tre ore. Mike dà a Charlie 1 tavoletta di cioccolato e 4 caramelle. Per quanto tempo potrà scorrazzare con la bicicletta di Charlie?

10Quali sono le quattro cifre che bisogna togliere dal numero 4921508, senza cambiare l'ordine, per ottenere il numero di tre cifre minore possibile?

11Quanti numeri di due cifre sono divisibili simultaneamente per 2 e per 7?

12Se A + 1 = B + 2 = C – 3 = D + 4 = E – 5 qual è il maggiore?

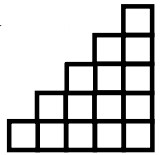
13Quanti quadratini formeranno una figura simile a quella di sotto ma con 10 scalini?

14Cinque vicini hanno dei terreni rettangolari identici. Ognuno di essi ha piantato una siepe (indicata in figura con un tratto continuo) sul proprio terreno per proteggere la parte del giardino con i fiori. Chi ha utilizzato una siepe più lunga?

15Alberto viene al Club tutti i giorni, Bob ogni due giorni, Cloe ogni tre giorni, Dan ogni quattro giorni, Enrico ogni cinque giorni, Franco ogni sei giorni e Gabriele ogni sette giorni. Oggi sono tutti presenti, fra quanti giorni saranno ancora nuovamente tutti insieme?

16L’addestratore degli elefanti del Circo Kang impiega 40 minuti per lavare un elefante. Il suo giovane figlio impiega 2 ore per fare lo stesso lavoro. Quanto tempo impiegheranno l’addestratore ed il proprio figlio per lavare tre elefanti, se essi lavorano insieme?

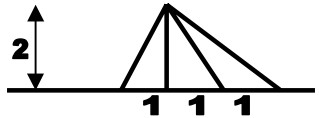
17La somma delle aree di tutti i triangoli che si possono vedere nella figura è:

18Ogni salto di mamma kangourou è lungo 3 metri e dura 1 secondo; ogni salto del suo piccolo figlio è lungo 1 metro e dura mezzo secondo. Entrambi i kangourou partono saltando simultaneamente dallo stesso posto verso un albero di eucalipto. La distanza tra il punto di partenza e l'albero è di 180 metri. Quanti secondi dovrà attendere mamma kangourou all'albero l'arrivo del proprio figlioletto?

1996 ragazzi in un campeggio estivo sono stati suddivisi in vari gruppi, in modo che ogni gruppo sia formato dallo stesso numero di ragazzi. In quanti modi differenti si può realizzare questa suddivisione, se ogni gruppo deve contenere più di 5 e meno di 20 ragazzi?

20Qual è l'angolo al centro di un settore la cui area è il 15 % dell'area dell'intero cerchio?

21800 dobloni hanno lo stesso valore di 100 ducati. 100 dobloni hanno lo stesso valore di 250 talleri. Quanti ducati hanno lo stesso valore di 100 talleri?

22Mamma Chiara compera una scatola di zucchero in zollette. Cristina mangia lo strato superficiale, cioè 77 zollette; di quello che resta mangia lo strato laterale, che consiste in 55 zollette; infine Cristina mangia lo strato frontale. Quante zollette sono rimaste nella scatola?

23Ad una gara di danza tutti i giudici esprimono il loro voto ai candidati con voti interi. La media di tutti i punteggi per un candidato è stata di 5.625. Qual è il numero minimo di giudici perché ciò sia possibile?

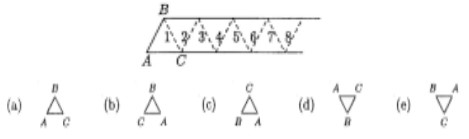
24La figura rappresenta una lunga striscia di carta divisa in 2000 triangoli, con le linee tratteggiate. Supposto che la striscia possa essere ripiegata secondo le linee tratteggiate, nell'ordine indicato dai numeri, in modo che la parte destra della striscia conservi sempre la posizione orizzontale e che la porzione ripiegata dalla sinistra vada a sovrapporsi al triangolo immediatamente adiacente a destra. In quale posizione si troveranno i vertici A, B, C dopo 1999 ripiegature?

25Vi sono tre scatole e tre oggetti: una moneta, una conchiglia e un pisello. Ogni scatola contiene uno ed un solo oggetto: la scatola verde è a sinistra della scatola blu; la moneta si trova a sinistra del pisello; la scatola rossa è a destra della conchiglia; il pisello si trova a destra della scatola rossa; in quale scatola si trova la moneta?

26Se ogni lettera corrisponde ad una cifra differente, allora KANGAROO + 10000 × AROO – 10000 × KANG (× - indica l'ordinaria moltiplicazione) vale

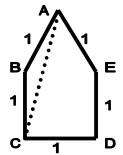
27Nella figura, l'angolo BÂC misura:

28Quanti sono i numeri interi tra 100 e 999 che hanno tutte le cifre differenti?

29Prendiamo un esagono regolare e disegniamo tutte le sue diagonali. Quanti angoli di 30° vediamo?

30Il corpo di un vermetto è fatto di cerchi. Quanti differenti tipi di questo vermetto esistono, se 3 delle 5 parti del corpo devono essere gialle e 2 devono essere verdi?