1Il kangourou calcola: 2 × 0 + 0 × 1. Il risultato è:

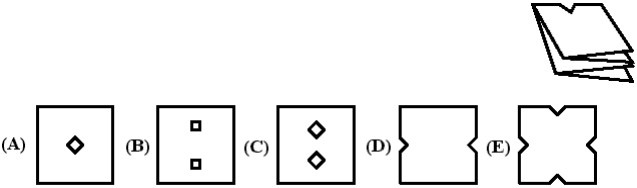
2Quale dei seguenti fogli corrisponde a quello piegato nella figura?

3Il vecchio orologio del nonno ritarda di 20 secondi ogni ora. Quale sarà il ritardo dell'orologio dopo 24 ore?

4Quanta parte di questa figura è colorata di nero?

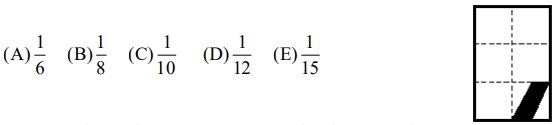
5Vi sono 108 poltrone in un aereo passeggeri. Vi è una poltrona vuota ogni due passeggeri. Quanti sono i passeggeri su quell'aereo?

6Enrico ha tre sorelle e cinque fratelli. Sua sorella Sabina ha 'S' sorelle e 'F' fratelli. Quanto vale il prodotto di S per F?

7In quale figura l'area della superficie colorata in grigio è maggiore?

8Chiara pensa un numero intero. Raddoppia tale numero, raddoppia ancora il risultato ottenuto, raddoppia ancora una volta e poi ancora una volta. Quale dei seguenti numeri certamente non può essere il risultato?

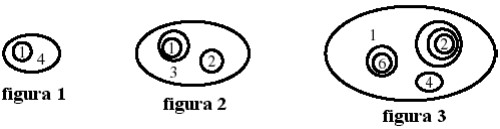
9Se si conviene che la figura 1 rappresenti il numero 14 e la figura 2 il numero 123, quale numero rappresenta la figura 3?

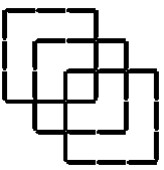
10Trova il minimo numero di fiammiferi che bisogna aggiungere alla figura in modo da ottenere esattamente 11 quadrati.

11Nikita e Sasha corrono sulla pista dello stadio. Nikita impiega 3 minuti per ogni giro, mentre Sasha impiega 4 minuti per ogni giro. Partono allo stesso momento. Dopo quanti minuti essi passeranno ancora la linea di partenza insieme?

12Edoardo ha 201 monete. Un terzo di queste sono monete da 1 Euro, un terzo sono monete da 5 Euro ed il resto sono monete da 10 Euro. Quanti Euro possiede Edoardo?

13Siamo alla finale dei 10 chilometri per le gare di atletica della scuola. Giorgio corre per 9 641 metri, 3 456 decimetri e 12 340 millimetri e dopo questa distanza crolla a terra esausto e non riesce più a continuare. Quanti centimetri gli mancano per raggiungere la linea di arrivo?

14Qual è il numero dell'ultimo vagone del trenino del kangourou?

15Se il drago rosso avesse 6 teste in più del drago verde, essi avrebbero in totale 34 teste. Ma il drago rosso ha 6 teste meno del drago verde. Quante teste ha il drago rosso?

16La lunghezza di un campo rettangolare è di 80 m e l'area è di 3 200 m². Trova la lunghezza di un altro campo rettangolare la cui area e la cui larghezza sono entrambe la metà delle corrispondenti del primo campo

17Susanna impiega esattamente un'ora per svolgere tutti i propri compiti a casa. Impiega un terzo del suo tempo con la matematica e due quinti del rimanente con geografia. Quanto tempo impiega per fare i compiti delle altre materie?

18Tre anni fa i tre gemelli Paolo, Simone e Billy con la loro sorella Susy, più 'vecchia' di loro di quattro anni, assommavano insieme 24 anni. Quanti anni ha Susy attualmente?

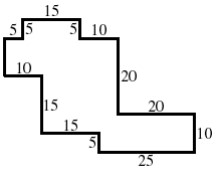
19Il giardino di Pamela ha la forma mostrata nella figura a fianco. Tutti gli angoli sono retti (90°), e le lunghezze dei singoli lati sono espresse in metri. Allora l'area del giardino, in metri quadrati, vale

20Durante le loro vacanze Alberto, Brenda e Cristina hanno guadagnato insieme 280 Euro. Alberto ha lavorato il doppio del tempo di Brenda e quattro volte il tempo di Cristina. Essi decidono di dividere i loro guadagni in modo imparziale. Quanti Euro toccano a Cristina?

21I sette bastoncini grigi nella figura hanno la stessa lunghezza; lo spazio libero tra uno loro ed il successivo sulla stessa riga è sempre lo stesso. Qual è la lunghezza di ognuna delle due parti uguali segnate con un punto interrogativo?

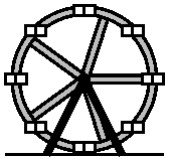
22La più grande attrazione di un Luna Park è la grande ruota panoramica (la figura ne mostra una similare ma più piccola). Le cabine sono equidistanti fra loro e numerate 1, 2, 3, … . Nel momento in cui la cabina n. 25 è nella posizione più bassa la cabina n. 8 è nella posizione più alta. Quante cabine vi sono su quella ruota panoramica?

23Un faggio vecchio di 100 anni produce 1,7 kg di ossigeno in un'ora. Quanti faggi di questo tipo sono necessari per fornire ossigeno per un'ora a 34 studenti, sapendo che ogni studente consuma in un'ora 0,7 kg di ossigeno?

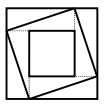
24Il quadrato più grande ha area 16, il più piccolo ha area 4. Qual è l'area del quadrato posto in posizione obliqua?

25In un comune dado la somma dei punti sulle facce opposte dà sempre sette. Cecilia costruisce una torre con sei dadi comuni uguali, incollando le facce come mostrato nella figura. Qual è il massimo numero di punti che Cecilia può ottenere sommando i valori ottenuti sulla superficie della torre?

26Sostituisci ad ogni lettera una cifra in modo che il risultato della moltiplicazione sia esatto 45 × A3 = 3BCD La somma delle quattro cifre inserite vale:

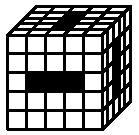
27In un cubo di lato 5, costruito accostando cubi di lato 1, sono stati effettuati dei fori (da una parte all'altra) come mostrato nella figura. Quanti cubi di lato 1 sono rimasti?

28La stella mostrata nella figura è stata realizzata toccando i punti medi dei lati di un esagono regolare. Se l'area della stella è 6, quale è l'area dell'esagono?

29Tutti i solidi seguenti, ottenuti accostando cubetti tutti uguali fra loro, hanno lo stesso volume. Quale ha la superficie totale maggiore?

30Usando una sola volta le cifre da 1 a 6, tu puoi formare due numeri di tre cifre (per esempio 645 e 321, che differiscono di 324). Cerca i due numeri di tre cifre la cui differenza sia la più piccola possibile. La più piccola differenza è: