1Quale delle seguenti operazioni fornisce il risultato maggiore?

2Tommaso ha 9 biglietti da cento euro, 9 biglietti da 10 euro e 10 monete da 1 euro. Di quanti euro dispone?

3Quanti numeri interi sono compresi tra 2,09 e 15,3?

4Somma il più piccolo intero positivo divisibile per 2 e per 3 al più piccolo intero positivo divisibile per 2, per 3 e per 4. Ottieni

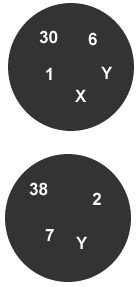
5La somma dei numeri in ciascuno dei due anelli in figura deve essere 55. Quale numero si deve sostituire alla lettera X?

6Quanto fa?

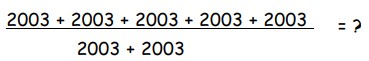
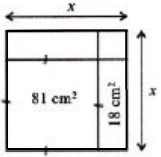
7Osserva la figura. Quanto vale la misura x del lato del quadrato più grande?

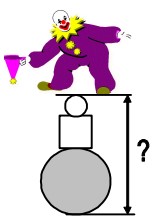
8La figura mostra il clown Davide che balla sulla sommità di due palle con in mezzo un cubo. Il raggio della palla inferiore è di 6 dm mentre il raggio della palla superiore è un terzo di esso. Il lato del cubo è di 4 dm più lungo rispetto al raggio della palla superiore. Qual è l'altezza dal suolo della costruzione sulla quale danza il clown?

9L’età media dei giocatori di una squadra di calcio presenti in campo (in numero di 11) all’inizio di una partita è 23 anni. All’inizio del secondo tempo due giocatori, entrambi di 26 anni, vengono sostituiti da un giocatore di 20 e da uno di 21 anni. Dopo queste sostituzioni, qual è la nuova età media della squadra?

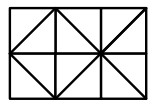
10Quanti dei triangoli, individuabili nella figura, hanno area uguale a quella di ciascuno dei 6 quadrati (uguali) che, accostati, formano il rettangolo?

11Quale data sarà 2003 minuti dopo le 20.03 del 20-03-2003?

12Scegliendo in tutti i modi possibili due numeri diversi tra 1, 2, 3, 4, 5 e sommandoli, quanti diversi risultati possiamo ottenere?

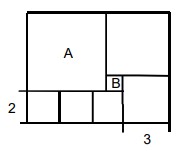
13Il rettangolo in figura è costruito accostando 7 quadrati, per alcuni dei quali è indicata la misura del lato. Il quadrato A è quello di area maggiore, mentre il quadrato B è quello di area minore. Quanti quadrati come B possono essere contenuti, senza sovrapposizioni, nel quadrato A?

14Elisabetta ha 20 biglie di colori differenti: giallo, verde, blu e nero. 17 biglie non sono verdi, 5 sono nere, 12 non sono gialle. Quante sono le biglie blu di Elisabetta?

15Lungo la strada dalla casa di Luigi alla piscina ci sono 46 alberi. Andando da casa in piscina e ritornando, Luigi ha contrassegnato alcuni alberi con un nastro rosso come segue. All’andata ha segnato il primo albero e successivamente il secondo di ogni coppia di alberi che incontrava; al ritorno invece ha segnato il primo albero e successivamente il terzo di ogni terna di alberi che incontrava. Dopo di ciò quanti alberi hanno il nastro rosso?

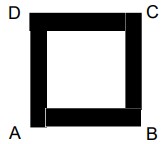
16Il quadrato ABCD in figura è formato da un quadrato interno (bianco) e da quattro rettangoli uguali colorati in grigio (accostati senza sovrapposizioni). Ogni rettangolo grigio ha il perimetro di 40 cm. Qual è l'area del quadrato ABCD?

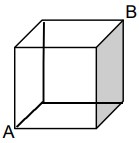
17Quanti sono i possibili differenti percorsi di minore lunghezza che, percorrendo i lati del cubo, uniscono il vertice A al suo opposto B? (vedi figura)

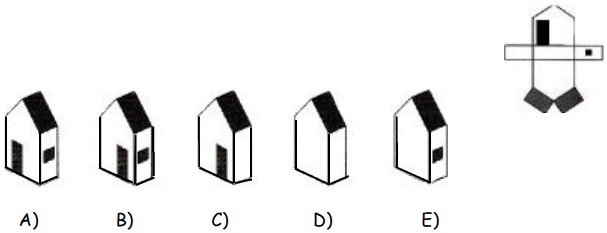
18Costruiamo una casetta a partire dal disegno a fianco riprodotto su un cartone. Quale casetta risulta impossibile ?

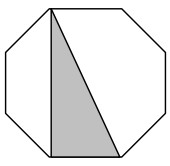
19Abbiamo un esagono regolare, ne scegliamo tre vertici a caso e consideriamo il triangolo individuato da questi tre vertici. Questo triangolo certamente non è

20L’ottagono regolare in figura ha area 36 m2. Quanto vale l’area del triangolo colorato in grigio?

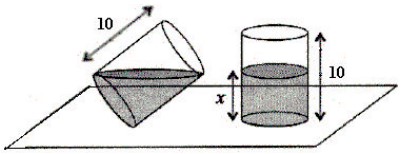
21Un bicchiere cilindrico trasparente alto 10 cm è riempito parzialmente con acqua. Voi potete vedere il bicchiere in due posizioni. Qual è l'altezza x dell'acqua nell'immagine a destra?

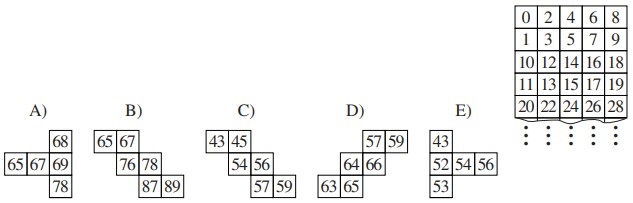
22Walter decide di riportare in una tabella tutti i numeri interi da 0 a 109, seguendo il criterio suggerito dalla figura a fianco. Quale dei tasselli seguenti non può assolutamente far parte della tabella di numeri di Walter?

23Tu disponi di sei bastoni di lunghezza 1 cm, 2 cm, 3 cm, 2001 cm, 2002 cm e 2003 cm. Devi sceglierne tre fra questi e formare un triangolo (che non si riduca ad un segmento). Quante sono le diverse scelte possibili di tre bastoni che puoi effettuare?

24In un fossato vi sono draghi completamente rossi e draghi completamente verdi. Ogni drago rosso ha 6 teste, 8 gambe e 2 code. Ogni drago verde ha 8 teste, 6 gambe e 4 code. Fra tutti i draghi si contano 44 code. ll numero delle gambe verdi è inferiore di 6 rispetto al numero delle teste rosse. Quanti sono i draghi rossi in quel fossato?

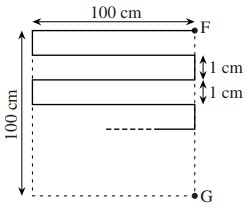
25Osserva la figura. Quanti cm separano A da B seguendo il percorso suggerito dal tratto continuo?

26Ad ogni simbolo corrisponde una e una sola delle cifre 0, 1, 2, ..., 9 e a simboli diversi corrispondono cifre diverse. Conosci il risultato della somma a sinistra. Qual è il risultato della somma a destra?

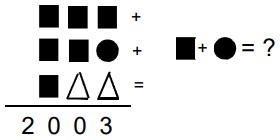
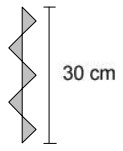
27La figura di sotto è formata da cinque triangoli rettangoli isosceli uguali. Trova l'area della parte colorata.

28Anna ha una scatola con 9 matite. Almeno una di queste è blu. Comunque prese 4 di quelle matite almeno due hanno lo stesso colore, e comunque prese 5 di quelle matite al più tre hanno lo stesso colore. Qual è il numero delle matite blu?

29In un paese si conoscono tutti: alcuni di essi mentono sempre, mentre gli altri dicono sempre la verità. Incontriamo un gruppo formato da 4 persone di questo paese e a ciascuna di esse chiediamo: quanti sono i mentitori fra di voi? Otteniamo le seguenti 4 risposte diverse: 0, 1, 2, 3. Quanti sono realmente i mentitori in quel gruppo di persone?

302003 è un numero primo. Oggi è il 20-03-2003: sopprimendo i trattini che separano il giorno dal mese dall’anno (e gli spazi relativi), scriveremmo 20032003, e questo numero è divisibile per 10001. Quanti giorni passeranno prima di arrivare alla prossima data che, seguendo lo stesso criterio, verrebbe rappresentata da un numero ancora divisibile per 10001?