1Quale dei seguenti numeri, espressi in forma di frazione, è il più grande?

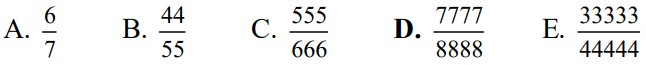
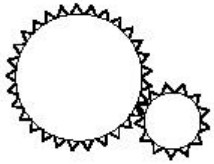
2In una macchina ci sono due ruote dentate disposte come quelle della figura. Il raggio della ruota più grande è 3 volte il raggio dell’altra. Che cosa succede alla ruota più piccola se la più grande fa un giro in verso antiorario (cioè nel verso opposto a quello delle lancette dell’orologio)?

3In un gioco bisogna contare da 1 a 100 e applaudire ogni volta che si incontra o un multiplo intero di 3 o un numero che termina per 3. Quante volte si dovrà applaudire?

4Il 1° di luglio a Newbury il sole sorge alle 4:53 e tramonta alle 21:25. Il mezzogiorno solare è quindi a metà tra questi due orari. A che ora è il mezzogiorno solare a Newbury il 1° di luglio?

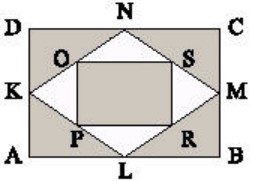
5Osserva la figura. K, L, M, N sono i punti medi del rettangolo ABCD; analogamente O, P, R, S sono i punti medi dei lati del quadrilatero KLMN. Quale frazione dell’area del rettangolo ABCD risulta ombreggiata?

6Quale delle seguenti espressioni fornisce il risultato maggiore?

7Alfonso il pasticcere produce 23 uova di Pasqua al giorno e riceve una richiesta di 2002 uova proprio in un giorno in cui non ha più uova in magazzino. Dopo quanti giorni (incluso il primo) Alfonso può soddisfare l’ordine e quante uova gli restano dopo aver spedito le 2002 uova?

8La faccia inferiore del dado in figura ha 6 punti, la faccia a sinistra ne ha 4, la faccia posteriore ne ha 2. Supponendo di non poter vedere più di tre facce contemporaneamente, qual è il massimo numero di punti che possono essere visti contemporaneamente rigirando il cubo?

9Fabio, Giulia, Mauro e Nadia possiedono ciascuno un solo animale. I loro animali sono un cane, un canarino, un gatto e un pesce rosso. L’animale di Mauro ha il pelo; quello di Fabio ha 4 zampe; Nadia ha un uccellino e sia Giulia sia Mauro non possiedono gatti. Quale delle seguenti affermazioni è falsa?

10Una cassetta di mele costa 2 €, una di pere costa 3 € e una di prugne costa 4 €. Se 8 cassette di frutta sono costate 23 €, quante di esse, al massimo, possono contenere prugne?

11a, b, c sono tre numeri tali che a : b = 9 : 4 e b : c = 5 : 3. Se ne deduce che (a-b) : (b-c) è uguale a

12Una nave raccoglie in mare 30 naufraghi. I viveri a bordo prima dell’incontro sarebbero stati sufficienti per 60 giorni, ma diventano sufficienti solo per 50 giorni appena i naufraghi mettono piede sulla nave. Supponendo che tutte le persone imbarcate consumino la stessa quantità di viveri, quante erano le persone a bordo prima dell’incontro con i naufraghi?

13Una certa colonia è costituita per il 25% da topi bianchi e per il 75% da topi neri. Tra i topi bianchi, il 50% ha gli occhi azzurri mentre tra i topi neri solo il 20% ha gli occhi azzurri. Sapendo che 99 topi hanno gli occhi azzurri, di quanti topi è composta la colonia?

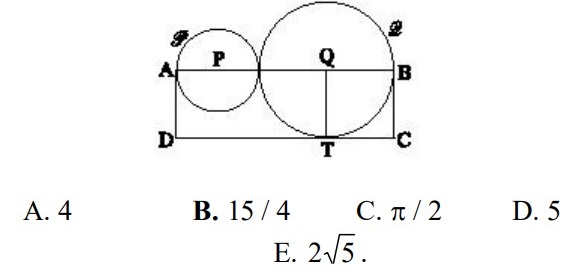
14In figura P e Q sono i centri di due circonferenze P e Q tangenti esternamente e la retta PQ taglia le due circonferenze in A e B (oltre che nel punto di tangenza). ABCD è un rettangolo con il lato DC tangente a Q nel punto T. Se l’area di ABCD è 15, quanto vale l’area del triangolo PQT?

15Cinque ragazzi salgono a coppie su una bilancia in tutte le combinazioni possibili. I pesi letti sono, in kg: 90, 92, 93, 94, 95, 96, 97, 98, 100, 101. Sommando i pesi dei cinque ragazzi si ottiene

16In Canada parte della popolazione parla solo inglese, parte solo francese e parte parla entrambe le lingue. Se l’85% della popolazione parla inglese e il 75% parla francese, quale percentuale della popolazione parla entrambe le lingue?

17I piatti P, Q e R sono allineati in ordine di peso crescente e si vuole aggiungere ad essi l’ultimo piatto, mantenendo questo tipo di ordinamento. Sapendo che oggetti di forma uguale hanno lo stesso peso, quale dei seguenti enunciati è corretto?

18La mamma vuol sapere chi dei suoi 4 figli ha nascosto il regalo per il compleanno del papà. Essi fanno le seguenti affermazioni: Aldo: “non sono stato io”; Bruno: “non sono stato io”; Carlo: “è stato Dino”; Dino: “è stato Bruno”. Se tutti tranne uno hanno detto la verità, chi ha mentito?

19In alcuni dei quadratini che compongono una griglia 2 x 9 ci sono delle monete. Ogni quadratino o contiene una moneta oppure ha un lato in comune con un quadratino che ne contiene una. Il numero di monete presenti sulla griglia deve essere almeno

20Il signor Rossi impiega 90 secondi per portarsi al sesto piano di un grande magazzino salendo a piedi i gradini di una scala mobile quando questa non è in funzione; ne impiega invece 60 quando la scala è in funzione, ma si lascia trasportare senza muoversi. Quanti secondi impiega se la scala è in funzione e contemporaneamente egli ne sale i gradini?

21Un numero intero positivo n è divisibile per 21 e per 9. Qual è il minimo numero di divisori interi positivi che deve avere n (1 e n inclusi)?

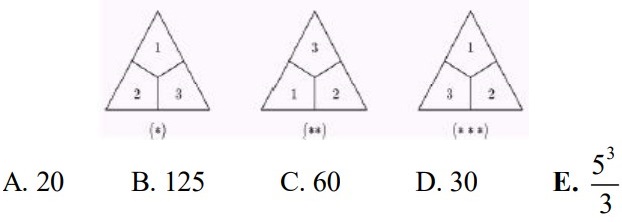
22Un gioco è composto da pezzi a forma di triangolo equilatero, ciascuno suddiviso in tre parti uguali, ciascuna colorata con colori diversi (v. figura, dove sono presenti tre pezzi e dove a numeri uguali corrispondono colori uguali). Se i colori disponibili sono 5 e nel gioco sono presenti tutte le possibili combinazioni di questi colori, quanti devono essere al minimo i pezzi distinti che compongono il gioco? Attenzione. I pezzi possono essere ruotati: quindi due pezzi che usino i colori 1, 2, 3 come quelli che in figura sono denotati con (*) e (**) sono da considerarsi uguali, ma diversi dal pezzo denotato con (***).

23In uno stesso mese tre domeniche sono cadute in giorni pari. Quale giorno della settimana era il 20 di quel mese?

24Il quadrante di un orologio si rompe in tre settori (cioè in tre parti, ciascuna costituita da un unico pezzo) in modo che ognuno dei numeri indicanti le dodici ore cada interamente all’interno di qualche settore. Sapendo che la somma dei numeri che si trovano in ciascun settore è la stessa per i tre settori, si può essere certi che

25Traccia nel piano due circonferenze diverse fra loro e tre rette diverse fra loro. Qual è il massimo numero di punti in cui si intersecano almeno due di questi enti geometrici?

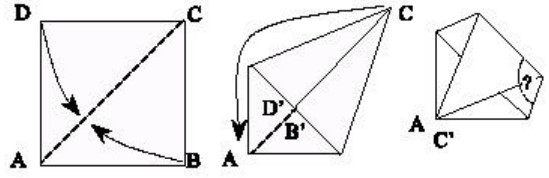
26Piegando un foglio di carta quadrato si è ottenuto un pentagono: prima il foglio è stato piegato, facendo perno nel vertice C, in modo da portare i lati BC e DC sulla diagonale AC e poi si è piegata la forma così ottenuta in modo da portare il vertice C sul vertice A (v. figura). Qual è l’ampiezza dell’angolo segnato con il punto di domanda?

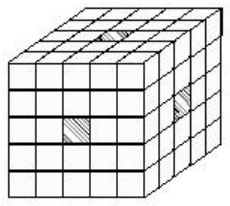
27Un cubo con un lato lungo 5 cm è formato di cubetti di lato 1 cm. Togliamo 3 file di cubetti come indicato dalla figura e immergiamo il solido che rimane in un vaso di pittura. Quanti cubetti hanno una sola faccia pitturata?

28Considera l’insieme di tutti i numeri interi di 4 cifre formati dalle cifre 1, 2, 3, 4, nessuna ripetuta. La somma di tutti i numeri di questo insieme vale

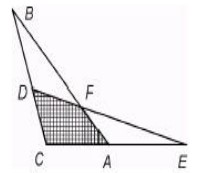
29In figura, i triangoli ABC e DCE sono uguali; inoltre la lunghezza di DC è 1 cm e quella di CB è 4 cm. Se l’area del triangolo ABC è S, allora l’area del quadrilatero AFDC vale

30Considera una successione di numeri interi positivi, tale che ogni numero dal terzo in poi sia la somma di tutti quelli che lo precedono, il primo numero sia 1 e l’ultimo sia 1000. Nella più lunga successione che si può costruire con questa legge, quanto vale il secondo numero?