1Quanto vale 2005 x 100 + 2005?

2Chiara sceglie un numero intero e lo moltiplica per 3: quale dei seguenti numeri non può essere il risultato?

3Vi sono 8 canguri nelle caselle della figura a destra. Trova il minimo numero di canguri a cui ti basta far cambiare casella se vuoi che ogni riga e ogni colonna della tabella contenga esattamente 2 canguri.

4In una famiglia vi sono 3 figli: 2 maschi e una femmina. I loro nomi iniziano con le lettere A, B e C. Tra le lettere A e B, una e una sola è l’iniziale del nome di un maschio e così pure tra le lettere B e C. Con quale lettera inizia il nome delle femmina?

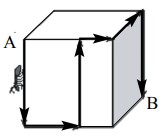
5In figura è rappresentato un cubo il cui spigolo misura 12 cm. Una formica si muove sulla superficie del cubo dal vertice A al vertice B lungo la traiettoria mostrata in figura. La lunghezza del percorso fatto dalla formica è

6Il 2005% di 200 vale

7Alla festa del mio compleanno eravamo in meno di 10. Ci siamo ripartiti i cioccolatini: ciascuno di noi ne ha avuti 12 e ne sono avanzati 8. Quanti erano i cioccolatini?

8Un falegname ha costruito una libreria alta 250 cm, ma ha posto i supporti per i ripiani su un lato a distanza di 20 cm l'uno dall'altro e sull'altro lato a distanza di 25 cm, sempre a partire dal basamento. Quanti ripiani perfettamente orizzontali può ospitare la libreria, basamento compreso?

9Una certa bevanda è preparata correttamente se è ottenuta mescolando 1 parte di sciroppo con 5 parti di acqua. Per errore Alfonso ha mescolato 5 parti di sciroppo con 1 di acqua, ottenendo 3 litri di miscuglio. Aggiungendo una opportuna quantità di acqua, Alfonso può ottenere una bevanda in cui sono rispettate le proporzioni stabilite. Quanti litri di acqua gli basta aggiungere?

10È stato commesso un furto in un magazzino e i ladri, per portarsi via la refurtiva, hanno dovuto usare un’auto. Dopo aver indagato, la Polizia ha concluso che i responsabili vanno ricercati fra Andrea, Bruno e Carlo. Si sa che Andrea non sa guidare e che Carlo agisce solo in compagnia di Bruno. Chi è sicuramente coinvolto nel furto?

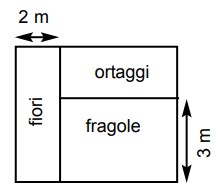
11Nel disegno vedi il giardino della famiglia Verdi: esso è rettangolare, ha un'area di 30 m2 ed è suddiviso in tre parti rettangolari. La parte in cui crescono i fiori ha il lato indicato lungo 2 m e area 10 m2. La parte coltivata a fragole ha il lato indicato lungo 3 m. Qual è l'area della parte coltivata a ortaggi?

12In un baule ci sono 5 valigie, ciascuna delle quali contiene 3 cassettine, in ognuna delle quali ci sono 10 monete d'oro. Baule, valigie e cassettine sono tutti chiusi con lucchetti. Qual è il minimo numero di lucchetti che ti basta aprire per avere 50 monete d'oro?

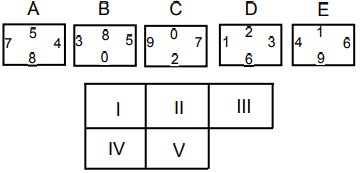
13In figura sono rappresentati 5 rettangoli di uguali dimensioni, ogni lato dei quali è etichettato con un numero intero. Devi sistemare questi rettangoli, traslandoli parallelamente a se stessi (cioè senza ruotarli e senza ribaltarli), nelle posizioni da I a V indicate, in modo che le etichette dei lati combacianti siano uguali. Quale dei rettangoli devi porre in posizione I?

14Se la somma di cinque numeri interi consecutivi maggiori di zero è 2005, il numero più grande è

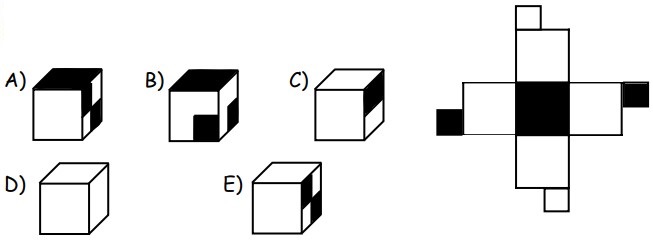
15Uno solo dei seguenti cubi ammette lo sviluppo presentato a destra. Quale?

16Supponi che uno sportello “Bancomat” fornisca solo banconote da 50, 20, 10 e 5 euro e che ne possa fornire di ogni tipo senza limitazioni. Supponi inoltre che, a ogni richiesta, il “Bancomat” fornisca sempre il minimo numero di banconote che consente di realizzare l’importo richiesto. Per dire in breve che il “Bancomat” ha erogato 3 banconote da 50 euro, 2 da 20 euro, nessuna da 10 euro e 1 da 5 euro scriviamo la sequenza [3, 2, 0, 1]. Quale fra le seguenti è la sequenza che indica quali banconote mi fornirà il “Bancomat” se richiedo 585 euro?

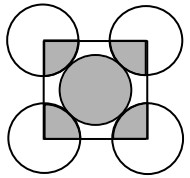
17I cinque cerchi rappresentati nella figura hanno lo stesso raggio e i 4 cerchi esterni sono tangenti a quello interno come mostrato. Il quadrato congiunge i centri dei quattro cerchi esterni. Allora il rapporto tra l'area della regione ombreggiata dei cinque cerchi e l’area della regione non ombreggiata dei quattro cerchi esterni è

18Quanti divisori diversi fra loro (inclusi 1 e 100) ha il numero 100?

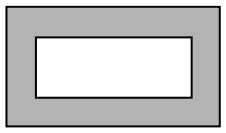
19Tutto intorno ad un'aiuola rettangolare c'è un vialetto che, lungo i lati, ha sempre la stessa larghezza (vedi figura). Il perimetro esterno del vialetto è più lungo di 16 m rispetto a quello interno. Quanto è largo il vialetto?

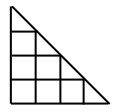
20Conta quanti triangoli e quanti quadrati si possono individuare al massimo nella figura. Di quanto il numero dei triangoli è maggiore di quello dei quadrati?

21La somma delle cifre di un numero intero minore di 208359 (e maggiore di zero) può essere al massimo

22Da mezzogiorno a mezzanotte Snoopy dorme nella sua cuccia e da mezzanotte a mezzogiorno racconta favole. Sulla cuccia c'è un cartello che recita: «Due ore fa Snoopy stava facendo la stessa cosa che farà tra un'ora». Per quante ore al giorno ciò che è scritto sul cartello corrisponde al vero?

23In una classe vi sono 12 studenti seduti in 3 file di 4 banchi ciascuna. Gli studenti si stringono la mano in base al criterio seguente: se due studenti sono seduti in banchi adiacenti (diagonali incluse), si stringono la mano una e una sola volta. Quante sono in totale le strette di mano?

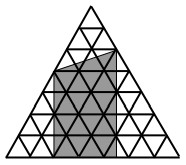
24L’area di ognuno dei piccoli triangoli equilateri in figura è 1 cm2. Qual è l'area in cm2 della regione ombreggiata?

25Biancaneve chiede a ciascuno dei 7 nani: «Quanti di voi mentono»? Il primo nano risponde «Uno», il secondo «Due» e così via fino al settimo che dice «Sette». Quanti dei sette nani mentono davvero?

26Dall’inizio del 2005 a tutto il 2025, quanti sono i mesi che iniziano e terminano con lo stesso giorno della settimana?

27Andrea ha guardato il suo orologio digitale da polso ieri sera alle 21:15 e ha notato che, coprendo i due punti con uno specchio perpendicolare al piano del quadrante, poteva ancora leggere l'ora esatta (due cifre sull’orologio e due nello specchio). Quante volte in un giorno succede la stessa cosa?

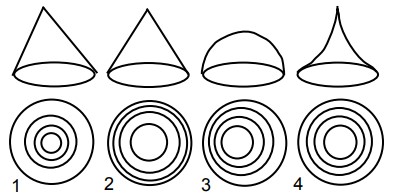
28A Kanglandia ci sono strane montagne: ne vedi le fotografie qui sotto sulla prima riga. Sulla seconda riga queste montagne sono rappresentate in una piantina che mette in evidenza i contorni delle sezioni di queste montagne con piani orizzontali che si immaginano tracciati alle seguenti quattro quote (ugualmente distanziate): 0, 250, 500, 750 metri sul livello del mare. Per un errore del cartografo le piantine non sono nelle stesso ordine delle foto. Sai riordinarle correttamente?

29Dora, Lara, Mara, Sara e Vera siedono su una panchina. Mara non siede all'estremità destra e Dora non siede all'estremità sinistra. Sara non siede a nessuna delle due estremità. Vera non è seduta vicino a Sara e Sara non è seduta vicino a Dora. Lara è seduta a destra di Dora, ma non necessariamente al suo fianco. Quale delle cinque ragazze è seduta all'estremità destra della panchina?

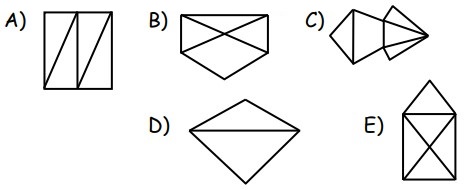
30Volendo tracciare le seguenti figure senza mai staccare la penna dal foglio, per una sola è necessario ripassare con la penna su qualche segmento già tracciato. Quale?