13x2005 = 2004 + 2006 + … . Quale dei seguenti numeri devi sostituire ai puntini per realizzare l'uguaglianza?

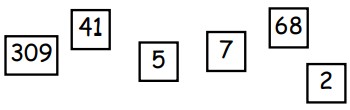
2Osserva la figura: sei numeri sono scritti su altrettanti foglietti. Accostando tutti i sei foglietti puoi formare dei numeri di dieci cifre. Qual è il più grande?

3Percorrendo il viale principale di Kangtown, osserviamo che ad ogni casa è assegnato uno (ed un solo) numero civico, dispari a quelle sul lato sinistro, pari a quelle sul lato destro. Sul lato sinistro i numeri vanno da 1 a 39; sul lato destro vanno da 2 a 34. Quante case vi sono lungo il viale?

4In un negozio di articoli sportivi di Stoccolma le combinazioni di oggetti illustrate hanno questi prezzi. Puoi acquistare anche ogni oggetto singolarmente. Quante corone costa uno di quei palloni da calcio?

5La metà di un centesimo è

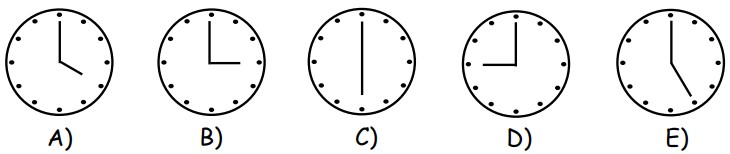
6Scegli la figura in cui il più piccolo dei due angoli formati dalle due lancette dell'orologio misura 150º

7Ogni volta che compare il simbolo ∇ nell’espressione 4∇2∇ − 13∇∇, si deve inserire una cifra (non necessariamente sempre la stessa); a seconda delle cifre inserite, la differenza che ne risulta può assumere valori diversi. Qual è il più piccolo di questi valori ?

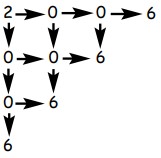
8Osserva la figura. In quanti modi possiamo scrivere il numero 2006 seguendo le frecce?

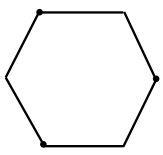
9La figura mostra un foglio di carta che ha la forma di un esagono regolare. Esso viene piegato in modo che i tre vertici indicati con un pallino vadano esattamente al centro dell'esagono e gli altri rimangano fermi. Che figura si ottiene?

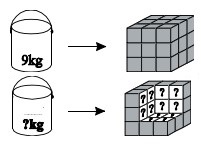
10Occorrono 9 chilogrammi di vernice per colorare l'intera superficie di un cubo. Rimuoviamo dal cubo 8 cubetti, come indicato nella figura. Quanti chilogrammi di vernice occorrono per colorare la parte rimasta bianca?

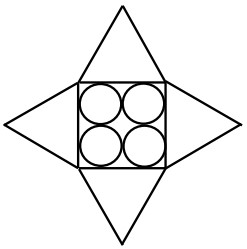
11Nella stella in figura compaiono quattro cerchi, un quadrato e quattro triangoli. I triangoli sono equilateri; i cerchi sono uguali, si toccano senza sovrapporsi e toccano i lati del quadrato. Se il raggio di ciascun cerchio è di 5 centimetri, quanto misura in centimetri il perimetro della stella?

12Considera solo i numeri interi maggiori di 0. Quanto vale la differenza tra la somma dei primi 1000 numeri pari e la somma dei primi 1000 numeri dispari?

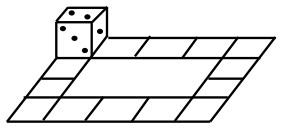
13Un dado si trova nella posizione indicata in figura. Quanti giri completi della pista occorreranno perché il dado, ruotando ogni volta di una faccia, ritorni esattamente nella posizione iniziale?

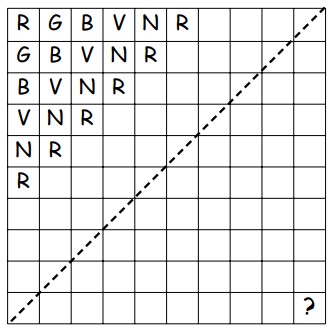
14Il quadrato in figura è suddiviso in 10 x 10 quadratini. Coloriamo ciascuno di essi assegnando uno stesso colore a tutti i quadratini che stanno su una stessa linea parallela alla diagonale evidenziata; usiamo i cinque colori disponibili nel seguente ordine: rosso, giallo, blu, verde, nero, rosso, giallo, blu, ... e così via (vedi figura). Quale sarà il colore assegnato al quadratino nell'angolo in basso a destra?

15Lungo una linea ferroviaria a doppio binario due treni viaggiano uno incontro all'altro, uno alla velocità costante di 80 km/h, l'altro alla velocità costante di 60 km/h. In questo istante distano 140 km. Fra quanto tempo, dopo essersi incrociati, la loro distanza tornerà ad essere di 140 km, se continuano a viaggiare alla medesima velocità?

16Qual è il risultato della sequenza di operazioni indicate nel riquadro?

17Hai un cubo e vuoi colorarne tre facce in blu e tre in rosso. In quanti modi diversi puoi farlo? (Due cubi si intendono colorati in modo diverso se, comunque se ne ruoti uno, non si può ottenere l'altro.)

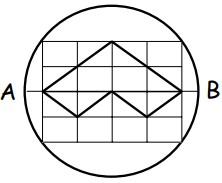
18Il diametro AB del cerchio in figura misura 10 cm. Quanto misura il perimetro della regione evidenziata, se i rettangoli più piccoli in figura sono tutti uguali?

19Avevo una corda lunga 15 metri. Tagliandola opportunamente, ne ho ottenuto degli spezzoni aventi per lunghezza un numero intero di metri. Il numero di spezzoni è il massimo possibile, compatibilmente con il fatto di non averne due della stessa lunghezza. Quanti tagli ho effettuato?

20Un segmento OE è lungo 2006 metri. Su di esso individuiamo tre punti A, B, C in modo che i segmenti OA e BE misurino 1111 metri e la lunghezza di OC sia il 70% di quella di OE. Partendo dall'estremo O, in quale ordine si trovano i cinque punti?

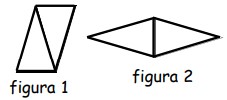
21Nelle figure 1 e 2 sono rappresentati due quadrilateri, ciascuno costruito accostando gli stessi due triangoli isosceli uguali fra loro: il primo è un parallelogramma, il secondo un rombo. Il perimetro del parallelogramma è di 3 centimetri più lungo del perimetro di ogni triangolo; invece il perimetro del rombo è di 7 centimetri più lungo di quello di ogni triangolo. Allora il perimetro di ogni triangolo vale, in centimetri,

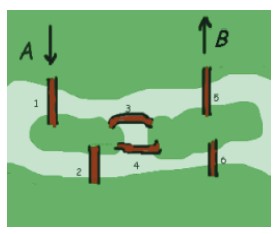
22Un fiume attraversa una città e vi sono due isolotti; vi sono anche sei ponti come mostrato nella figura. Quanti sono i percorsi differenti che permettono di andare dal punto A al punto B passando una ed una sola volta su ogni ponte?

23Considera una semiretta con origine O ed un punto A su di essa: se la distanza in centimetri di A da O vale a, diremo che a rappresenta il punto A. Quale dei seguenti insiemi di tre numeri rappresenta tre punti della semiretta uno dei quali abbia la stessa distanza da ciascuno degli altri due?

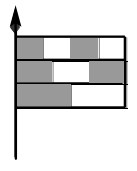
24Una bandiera è formata da tre strisce della stessa ampiezza, suddivise rispettivamente in due parti uguali, in tre parti uguali e in quattro parti uguali, come vedi in figura. Quale frazione della superficie della bandiera è colorata di grigio?

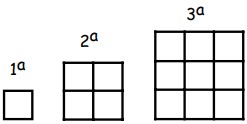
25Bianca costruisce griglie di stuzzicadenti ampliando ogni volta la griglia già presente con l'aggiunta di nuovi stuzzicadenti, secondo lo schema illustrato in figura. Quanti stuzzicadenti dovrà aggiungere Bianca alla 30-esima griglia per ottenere la 31-esima?

26Qual è il più piccolo numero di punti che basta togliere dalla figura mostrata a fianco, perché non ne restino tre che siano i vertici di qualche triangolo equilatero?

27In un campeggio, Aldo e Bruno preparano un fuoco per cuocere i loro alimenti, usando 15 pezzi di legno uguali: 8 sono stati portati da Aldo e 7 da Bruno. Carlo chiede di poter utilizzare lo stesso fuoco per cucinare e ricompensa gli amici con 30 monete, tutte dello stesso valore. Il modo equo di ripartire le monete tra Aldo e Bruno è:

28Le lettere M, A e T rappresentano altrettanti numeri interi. Sai che l’espressione M x (A - T + A) fornisce come risultato un numero dispari. Quale delle seguenti affermazioni è vera?

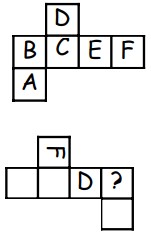
29Sulle facce di un cubo sono scritte sei lettere. La figura mostra due possibili sviluppi piani di quel cubo, nel secondo dei quali alcune lettere sono state omesse. Quale lettera dovrebbe essere scritta al posto del punto di domanda?

30Sulla lavagna sono scritti tutti i numeri naturali da 1 a 2006. Sottolineiamo prima tutti i numeri divisibili per 2, poi tutti quelli divisibili per 3 e infine tutti quelli divisibili per 4. Alcuni numeri risulteranno sottolineati più volte. Quanti numeri risulteranno sottolineati esattamente 2 volte?