1Quanti numeri interi sono compresi fra 2,009 e 19,03?

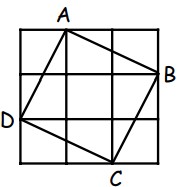
2Il quadrato più grande in figura, ottenuto accostando 9 quadratini, contiene il quadrato ABCD nella posizione indicata. Questo, a sua volta, copre per intero uno solo dei 9 quadratini, quello centrale. Qual è il massimo numero di quadratini che possono essere coperti dal quadrato ABCD se lo si dispone in modo opportuno?

3Cancellando alcune cifre del numero 12323314, vuoi ottenere un numero che non cambia quando viene letto da destra a sinistra invece che da sinistra a destra. Qual è il minimo numero di cifre cancellando le quali puoi raggiungere il tuo scopo?

4Le dieci cifre in figura sono costruite accostando opportunamente degli stuzzicadenti tutti uguali fra loro. Fra i numeri di due cifre, ho costruito quello che richiede l’impiego della maggiore quantità di stuzzicadenti. Quanti ne ho usati?

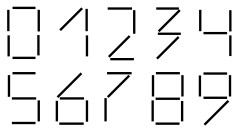
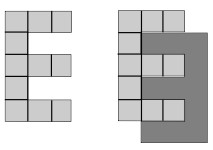
5La lettera “E” che vedi in figura a sinistra è stata ottenuta accostando 11 quadrati di 1 cm di lato. Accostando due di queste “E” uguali come è indicato nella figura a destra, ottieni una nuova figura. Il perimetro di questa nuova figura, rispetto a quello della lettera “E”, è

6Se conservi il calendario del 2009, qual è il primo anno in cui lo potrai riutilizzare (nel senso che ogni mese inizierà con lo stesso giorno della settimana con cui inizia nel 2009)?

7Un ponte attraversa un fiume largo 120 metri e deborda da ciascuna delle due rive per un quarto della sua lunghezza. Quanti metri è lungo il ponte?

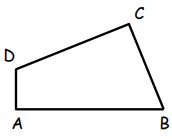
8Il rettangolo grande in figura è costruito accostando quadrati di tre misure diverse. Il lato di ciascuno dei quadrati più piccoli misura 20 centimetri. Quanti centimetri è lunga la linea evidenziata in grassetto?

9In una classe ogni alunno parla almeno una lingua fra tedesco e inglese. Gli alunni che parlano tedesco sono 15 e altrettanti sono gli alunni che parlano inglese. Almeno 6 alunni parlano entrambe le lingue. Allora il numero di alunni in quella classe è

10Trova il resto della divisione per 8 del numero 1 x 2 x 3 x … x 29 x 30 + 17

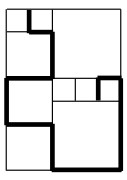
11La figura mostra cinque intrecci di corde. Quali di essi non possono essere realizzati con un unico spezzone di corda?

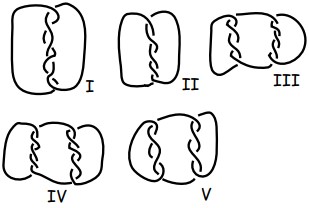
12Nel quadrilatero ABCD che vedi in figura le lunghezze dei lati, in metri, sono le seguenti: l(AB) = 11, l(BC) = 7, l(CD) = 9, l(DA) = 3. Inoltre, gli angoli in A e in C sono retti. Qual è, in metri quadrati, l’area del quadrilatero?

13In una scuola di danza attualmente vi sono 39 ragazzi e 23 ragazze. A partire da oggi, ogni settimana si aggiungeranno 6 ragazzi e 8 ragazze e fra alcune settimane il numero delle ragazze sarà uguale al numero dei ragazzi. Quanti tra ragazzi e ragazze saranno in quel momento presenti nel gruppo?

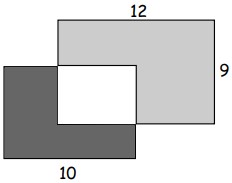
14Due rettangoli, uno 8 x 10 e l’altro 9 x 12 (le misure sono in metri), sono parzialmente sovrapposti come indicato dalla figura. L’area della regione in grigio scuro è 37 m2. Qual è, in metri quadrati, l’area della regione in grigio chiaro?

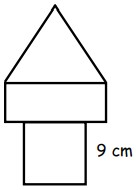
15La figura è formata accostando un quadrato, un rettangolo e un triangolo equilatero che hanno tutti lo stesso perimetro. Il lato del quadrato misura 9 cm. Qual è, in centimetri, la lunghezza del lato più corto del rettangolo?

16Abbiamo una scatola a forma di parallelepipedo rettangolo con misure, in centimetri, 24 x 24 x 60. Vogliamo riempirla completamente con cubi indeformabili tutti uguali fra loro, di cui possiamo scegliere la misura. Qual è il più piccolo numero di cubi che è sufficiente per raggiungere lo scopo?

17Carlo deve leggere un libro di 290 pagine. Ha programmato il suo compito come segue: leggerà 4 pagine ogni giorno, eccetto di domenica, giorno in cui ne leggerà sempre 25. Se inizierà la lettura domenica prossima e rispetterà il programma (quindi senza mai saltare giorni), quanti giorni impiegherà a terminare il libro?

18Alessia, Bruno, Celestina e Davide si sono classificati (non in quest’ordine) nei primi quattro posti di una gara. La somma dei numeri dei piazzamenti ottenuti da Alessia, Bruno e Davide è 6. Anche la somma dei numeri dei piazzamenti ottenuti da Bruno e Celestina è 6. Chi ha vinto la gara?

19Enrico ha 2009 piastrelle quadrate, tutte uguali fra loro. Usandole ogni volta tutte, quante diverse superfici rettangolari può piastrellare? (Due superfici vanno considerate diverse solo se è diversa la lunghezza di almeno uno dei due lati.)

20Considera le seguenti quattro affermazioni riguardanti uno stesso numero intero positivo. 1)È divisibile per 5; 2)È divisibile per 11; 3)È divisibile per 55; 4)È minore di 10; Sai che due di esse sono vere e le altre due sono false. Allora quel numero è

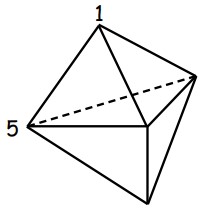
21Il solido in figura ha 6 facce, tutte triangolari. Ad ogni suo vertice viene associato un numero in modo che la somma dei numeri associati ai tre vertici di ogni singola faccia sia la stessa per tutte le facce. La figura indica i numeri associati a due dei vertici. Quanto vale la somma di tutti i numeri impiegati?

22Otto carte numerate da 1 a 8 sono riposte in due scatole, X e Y, in modo che la somma dei numeri riportati sulle carte sia la stessa nelle due scatole. Nella scatola X vi sono tre carte. Allora possiamo affermare con certezza che

23Le camere di un albergo sono numerate con numeri di tre cifre: la prima indica il piano e le rimanenti due indicano il numero della camera su quel piano. Per esempio, la camera 124 è la camera 24 del primo piano. L’albergo ha 5 piani numerati da 1 a 5 e ogni piano ha 35 camere numerate da 01 a 35. Quante volte è stata usata la cifra 2 per numerare tutte le camere?

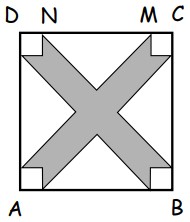
24Osserva la figura. ABCD è un quadrato il cui lato misura 10 cm; la distanza fra i punti N e M è di 6 cm. Ciascuna delle regioni non ombreggiate è un triangolo rettangolo isoscele o un quadrato. I quattro triangoli sono uguali fra loro e così pure i quattro quadrati. Quanto vale, in centimetri quadrati, l’area della regione ombreggiata?

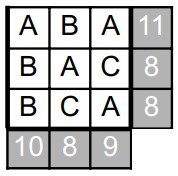
25Osserva la figura. Le tre lettere A, B e C rappresentano altrettanti numeri le cui somme, per righe e per colonne, sono quelle indicate (a destra per le righe e in basso per le colonne). Quanto vale A + B - C ?

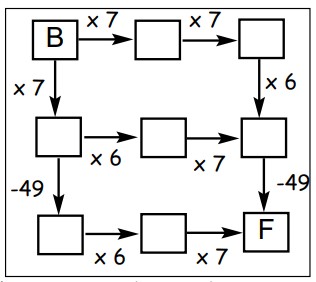
26Pensa ad un numero intero e mettilo nella casella B. Segui ora uno dei possibili cammini indicati dalle frecce eseguendo le operazioni corrispondenti. Se scegli opportunamente il numero con cui iniziare, ti sarà possible arrivare nella casella F con il numero 2009?

27Un set completo per il gioco del domino è costituito da 28 tessere tutte diverse fra loro: ogni tessera rappresenta uno dei 28 abbinamenti possibili di due numeri interi da 0 a 6 (inclusi quelli nei quali il numero viene ripetuto) e i numeri sono indicati mediante la corrispondente quantità di pallini. Qual è il numero complessivo dei pallini presenti in un set di questo tipo?

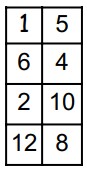
28In una tabella 4 x 2 due diversi numeri interi positivi sono stati inseriti nella prima riga. Ogni riga successiva contiene la somma e la differenza (maggiore meno minore) dei due numeri scritti nella riga precedente: rispettivamente, sotto il minore si scrive la somma e sotto il maggiore la differenza. In una tabella 11 x 2, costruita allo stesso modo, i numeri dell’ultima riga sono 64 e 96. Qual è la somma dei numeri della prima riga?

29Nel paese di Piedistrani ogni abitante ha il piede sinistro più lungo rispetto al piede destro: gli uomini più lungo di due numeri e le donne di uno. I negozi, tuttavia, sono come nel resto del mondo: vendono scarpe a coppie, una scarpa destra e una sinistra dello stesso numero. Per risparmiare, alcuni amici di Piedistrani, tra cui un nostro conoscente X di cui conosciamo sesso e numeri delle scarpe, decidono di associarsi e di comprare le scarpe tutti insieme, per poi accoppiarle nel modo che a loro conviene. Così facendo, ognuno prende due scarpe e rimangono inutilizzate una scarpa del numero 36 e una del numero 45. Vogliamo determinare il massimo numero di amici che potrebbero essersi accordati. Questo numero

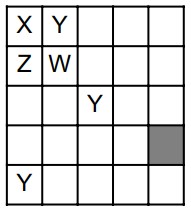
30Vogliamo colorare le celle della griglia in figura usando i quattro colori diversi X, Y, Z, W, in modo che due celle che sono a contatto non ricevano mai lo stesso colore (due celle si considerano a contatto se hanno in comune almeno un vertice). La figura mostra che alcuni colori sono già stati assegnati. Con quali colori può essere colorata la cella ombreggiata?