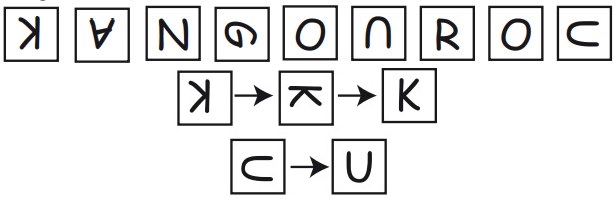
1Paolo ha alcune carte su ciascuna delle quali compare una lettera e le ha allineate come ti mostra la prima figura. Perchè la parola KANGOUROU appaia scritta correttamente, occorre però che alcune carte vengano ruotate, in qualche verso, una o due volte di 90 gradi. La seconda figura ti mostra le rotazioni da eseguire sulla lettera K e su una delle lettere U. Quante rotazioni di 90 gradi devono essere eseguite in totale perchè la scrittura appaia corretta?

2Una torta pesa 900 grammi. Luisa la taglia in quattro fette, la più grande delle quali pesa quanto le altre tre messe insieme. Quanti grammi pesa la fetta più grande?

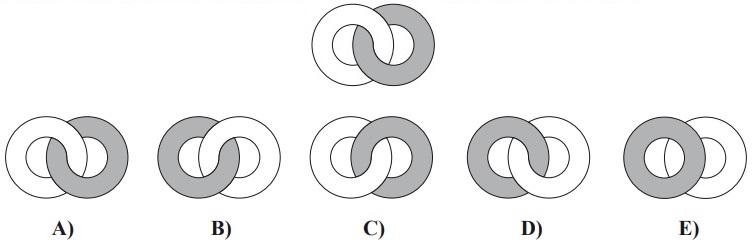
3Pietro e Paolo sono uno di fronte all’altro, separati da un vetro verticale trasparente su cui sono incollati due anelli, uno bianco e uno grigio, allacciati l’uno all’altro. La figura ti mostra come li vede Pietro. Come li vede Paolo?

4Nella addizione che ti mostriamo, le cifre centrali di ogni addendo sono state sostituite dal simbolo di dollaro. Qual è la somma di queste cifre?

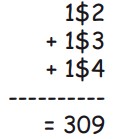
5Quanto vale la differenza fra il più piccolo numero intero di cinque cifre e il più grande numero intero di quattro cifre?

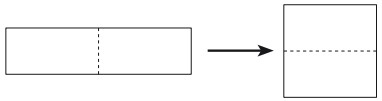
6Osserva quello che ti suggerisce la figura: un certo rettangolo è tale che, se viene tagliato a metà e le due metà vengono poste una sopra l’altra, si forma un quadrato. L’area del quadrato è 144 cm2 . Quanti centimetri è lungo il perimetro del rettangolo?

7Caterina ha 62 fiammiferi tutti uguali fra loro. Usandoli tutti, senza spezzarli, li ha disposti in modo da formare alcuni (uno o più) triangoli equilateri e un quadrato, che non hanno punti comuni. Per ogni lato di un triangolo ha usato 6 fiammiferi. Quanti ne ha usati per ogni lato del quadrato?

8La collana di Franca che vedi in figura contiene perle grigie e perle bianche. Franca vuole regalare a Bruna cinque delle perle grigie, sfilandole dalle estremità. Poiché inserire di nuovo le perle richiede molto tempo, Franca vuole sfilare, insieme alle grigie, il minor numero di perle bianche che le consenta di raggiungere lo scopo. Qual è questo numero?

9Cecilia ha inserito i numeri 6, 7, 8 e 9 nei quadrati bianchi in figura, uno per ogni quadrato, in modo da ottenere come risultato, una volta eseguite le operazioni indicate, il numero più alto possibile. Qual è questo numero? (Prima va eseguito il prodotto, poi la somma).

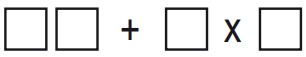
10L’orologio digitale di Bianca è parzialmente danneggiato: tutte e tre le linee orizzontali della cifra più a destra (quella dei minuti) non si illuminano. L’orologio è appena scattato dall’immagine mostrata a sinistra a quella mostrata a destra. Che ore sono in questo momento?

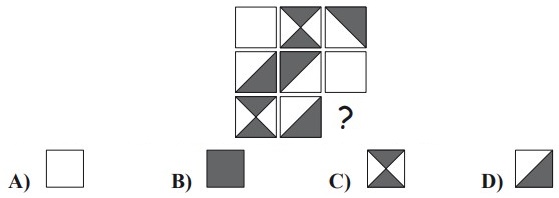
11Guido ha composto il piccolo mosaico che vedi in figura e può scegliere una fra quattro piastrelle rimaste per completarlo. Vuole che, una volta completato, la parte nera abbia la stessa area della parte bianca. Quale piastrella deve mettere al posto del punto di domanda?

12Elena e Simona vivono in una zona di pianura completamente piatta. Le due amiche incominciano a camminare da uno stesso punto, ma seguono percorsi diversi. Elena fa 1 Km verso nord, poi 2 Km verso ovest, poi 4 Km verso sud e infine 1 Km ancora verso ovest e si ferma ad aspettare Simona. Simona invece fa 1 Km verso est, poi 4 Km verso sud, poi 4 Km verso ovest: dal punto dove è arrivata, quanta strada e in quale direzione dovrà fare ancora Simona per arrivare dove è arrivata Elena?

13Al campo estivo, 7 ragazzi mangiano il gelato tutti i giorni, 9 ragazzi mangiano il gelato un giorno si e uno no mentre i ragazzi rimanenti non mangiano mai il gelato. Ieri hanno mangiato il gelato 13 ragazzi. Quanti ragazzi mangeranno il gelato oggi?

14Qual è il massimo numero di rettangoli non quadrati, i cui lati misurino un numero intero di centimetri, che possono essere inseriti senza sovrapposizioni in un quadrato di 7 centimetri di lato?

15Accostando, eventualmente dopo averli ruotati e/o ribaltati, quattro dei pezzi seguenti si può formare un quadrato. Quale pezzo andrà scartato?

16Un numero intero ha tre cifre: se le moltiplichiamo fra loro otteniamo 135. Quanto otteniamo se le sommiamo?

17Un ristorante ha 16 tavoli; ogni tavolo è da 3, 4 o 6 posti. Il ristorante può ospitare complessivamente 72 clienti; nei tavoli da 3 o 4 posti possono accomodarsi complessivamente 36 clienti. Quanti sono i tavoli da tre posti?

18Cinque amiche, Ada, Bice, Carla, Dina ed Enrica sono sedute ad un tavolo rotondo, in verso orario partendo da Ada nell’ordine in cui te le abbiamo elencate. Ad un preciso istante, tutte tranne una, che non si muove, scambiano il loro posto con una delle due amiche sedute a fianco. La nuova disposizione è ora Ada, Enrica, Bice, Dina, Carla, in quest’ordine sempre partendo da Ada e sempre in verso orario. Chi è rimasta ferma?

19Miriam ha alcuni cioccolatini: sia che li raggruppi in gruppi da 3 sia che li raggruppi in gruppi da 5, gliene rimangono sempre 2. Quanti ne deve prendere ancora al minimo se vuole che, sia raggruppandoli in gruppi da 3 sia raggruppandoli in gruppi da 5, non gliene avanzi nessuno?

20Le facce di un cubo sono numerate da 1 a 6. Si sa che le facce 1 e 6 hanno in comune uno spigolo e che lo stessa cosa accade per le facce 1 e 5, 1 e 2, 6 e 5, 6 e 4, 6 e 2. Quale faccia è opposta alla faccia 4?

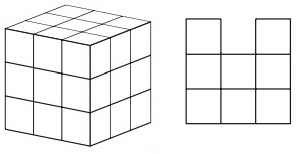
21In figura (a sinistra) vedi un cubo formato accostando 27 cubetti uguali fra loro. Vuoi rimuovere alcuni cubetti in modo che, guardando il cubo da ciascuna delle facce che appaiono nella figura (cioè da sopra, di fronte e da destra) ti appaia sempre l’immagine a destra. Qual è il minor numero di cubetti levando i quali puoi raggiungere lo scopo?

22Su un disco sono incise di seguito cinque canzoni A, B, C, D e E: la A dura 3 minuti, la B 2 minuti e mezzo, la C 2 minuti, la D un minuto e mezzo, la E 4 minuti. Tra una canzone e la successiva non vi sono pause e, una volta terminata la E, il disco riprende immediatamente con la A. Pino è uscito di casa, senza fermare il disco, mentre veniva eseguita la canzone C ed è rientrato esattamente un’ora dopo. Quale canzone veniva eseguita mentre rientrava in casa?

23Quanti numeri interi (positivi) di due cifre sono divisori di 2014?

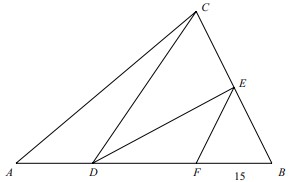
24Il triangolo ABC in figura è suddiviso nei quattro triangoli ADC, DEC, FED e FBE che hanno tutti la stessa area (la figura è solo indicativa). Il segmento FB è lungo 15 metri. Quanti metri misura il segmento AD ?

25Il re e i suoi messaggeri stanno viaggiando dal castello alla residenza estiva alla velocità di 5 Km all’ora. Ogni ora il re, dal punto in cui si trova, rimanda indietro al castello un messaggero che corre alla velocità di 10 Km all’ora. Quanti minuti passano fra l’arrivo al castello di un messaggero e del successivo?

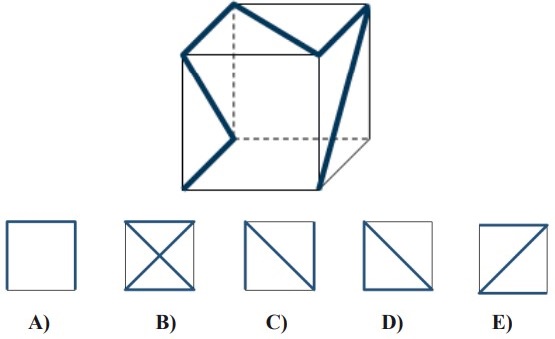
26Osserva la figura. Su un cubo di plastica trasparente è tracciata una linea decorativa, ricalcando alcuni degli spigoli e alcune diagonali di alcune facce. Per ciascuna delle sue facce, immagina di appiattire il cubo schiacciandolo perpendicolarmente su quella faccia (in questo modo, delle cinque facce che si muovono, solo la faccia opposta rimarrà intatta, mentre le altre quattro risulteranno compresse, ciascuna su uno dei lati di quella faccia). Ognuna delle seguenti immagini può allora essere ottenuta, tranne una. Quale?

27Sulla lavagna sono scritti tre numeri di una cifra ciascuno: la loro somma è 15. Aldo ne cancella uno e lo sostituisce con il numero 3: adesso il loro prodotto è 36. Qual è il numero cancellato da Aldo?

28Al coniglio Tim piacciono le carote e le carrube. Nei giorni in cui non è a dieta, mangia o 9 carote oppure 2 carrube oppure 4 carote e 1 carruba. Nei giorni in cui è a dieta, invece, mangia solo erba. Negli ultimi 10 giorni ha mangiato complessivamente 30 carote e 9 carrube. In quanti di questi 10 giorni ha mangiato solo erba?

29In uno strana regione del mondo, i due giorni che precedono ogni giorno di sole sono giorni di pioggia. In più, il quinto giorno dopo ogni giorno di pioggia è ancora un giorno di pioggia. Oggi in quella regione è un giorno di sole: per quanti giorni consecutivi a partire da domani, al massimo, possiamo prevedere se saranno di pioggia o di sole? (La risposta “1”, ad esempio, significa che possiamo predire il tempo di domani, ma non di dopodomani.)

30Una nonna ha dieci nipoti: oggi le loro età, in anni, sono dieci numeri tutti diversi fra loro e la loro somma è 180. Fra i dieci nipoti, Aldo è quello di età maggiore. Quanti anni deve avere, al minimo, oggi Aldo?