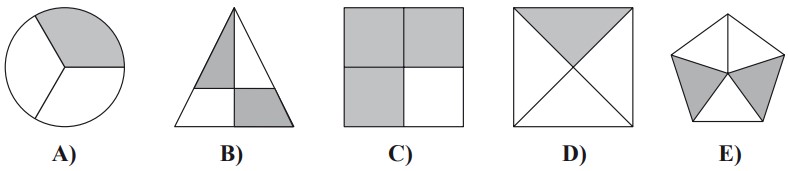
1In quale delle figure seguenti l’area della parte ombreggiata è metà dell’area totale?

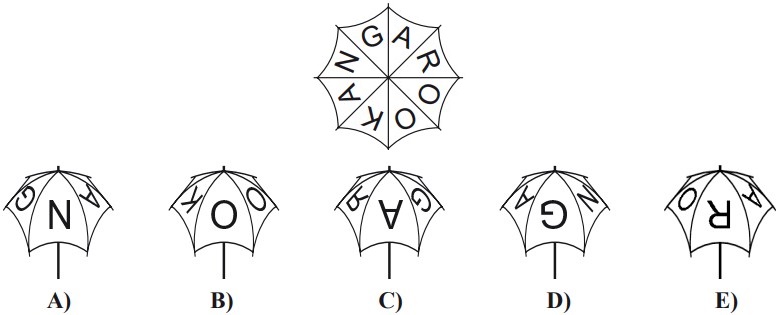
2Guardando il mio ombrello dall’alto, come mostrato nella figura, si legge la parola KANGAROO. Quale dei disegni nelle risposte mostra un ombrello che certamente non è il mio?

3Samuele ha dipinto i nove quadratini in cui è suddiviso il quadrato grande con vernice bianca, grigia e nera come vedi in figura. Ha poi deciso di ridipingerne alcuni in modo che due quadratini verniciati allo stesso modo non abbiano lati in comune. Qual è il numero minimo di quadratini che gli basta riverniciare?

4In un pollaio ci sono dieci galline. Cinque di esse fanno, ciascuna, un uovo al giorno mentre ciascuna delle altre fa un uovo a giorni alterni. Quante uova fanno complessivamente le galline in un periodo di 10 giorni?

5Quale delle frazioni seguenti fornisce un numero più piccolo di 2 ?

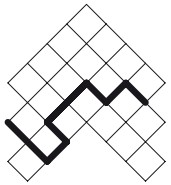
6L’area di ciascuno dei quadratini con cui è composta la figura misura 4 cm2. Qual è a lunghezza della linea evidenziata nella figura?

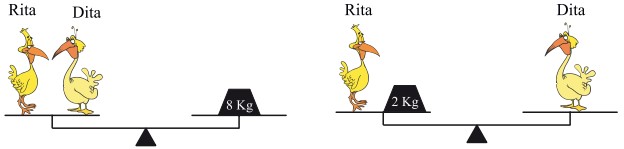
7Osserva le figure: quanto pesa Dita?

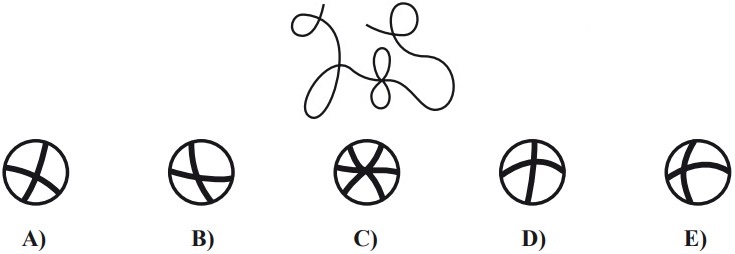
8Con una lente di ingrandimento Pietro esamina pezzo per pezzo questo disegno. Quale delle seguenti immagini non compare mai nella lente?

9Nel giardino di Giovanni ci sono solo piante di due tipi: quelle di un tipo hanno 5 foglie, le altre 2 foglie e 1 fiore. Giovanni ha scoperto che ci sono in tutto 32 foglie e 6 fiori. Quante sono in tutto le piante?

10Sara ha 4 strisce di carta tutte della stessa lunghezza. Ne incolla insieme due in modo che si sovrappongano per 10 cm ed ottiene un’unica striscia lunga 50 cm. Adesso vuole incollare le altre 2 in modo che esse formino una striscia lunga 56 cm. Di quanti centimetri deve farle sovrapporre?

11Tommaso accosta 6 quadrati uguali, di lato 1 cm, per formare la figura che vedi nel disegno. Quanti centimetri misura il perimetro della figura costruita da Tommaso?

12Ogni sera Maria scrive la data del giorno (senza l’anno) in cifre e poi calcola la somma delle cifre scritte. Ad esempio il 19 marzo scrive 19/03 e calcola 1 + 9 + 0 + 3 = 13. Qual è il numero più grande che riesce a scrivere in questo modo durante l’anno?

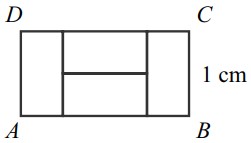
13Il rettangolo ABCD in figura è formato accostando 4 rettangoli uguali. Se la lunghezza di BC è 1 cm, quanto è lungo AB ?

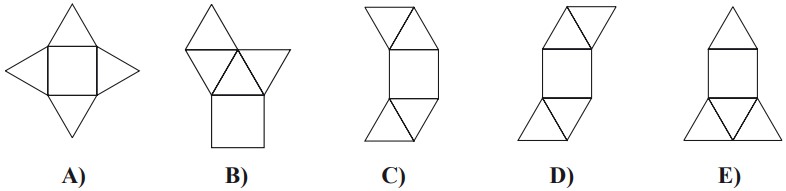
14Piegando opportunamente ciascuna di queste sagome di carta lungo i segmenti tracciati all’interno di essa, in un solo caso non si riesce ad ottenere una piramide. Quale?

15In Via del Salto ci sono solo 9 case, tutte su uno stesso lato della strada. In ogni casa vive almeno una persona, e il numero totale delle persone che vivono in una coppia di case adiacenti non supera mai 6. Un lattaio deve consegnare una bottiglia di latte per ogni persona che abita in Via del Salto. Qual è il numero minimo di bottiglie che deve mettere sul furgone per essere sicuro di averne abbastanza?

16Sia Lucia che la sua mamma sono nate in Gennaio. Oggi, 19 Marzo 2015, Lucia somma l’anno di nascita della mamma con l’età della mamma e poi somma al risultato il proprio anno di nascita e la propria età. Che numero ottiene?

17L’area di un rettangolo è 12 cm2 e le lunghezze (in cm) dei suoi lati sono numeri interi. Quale, tra i valori seguenti, può essere la lunghezza del perimetro del rettangolo?

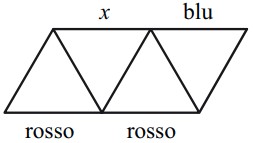
18Si deve colorare ognuno dei 9 segmenti in figura scegliendo tra i colori rosso, verde e blu e facendo in modo che, in ciascun triangolo, i 3 lati abbiano colori diversi. Come vedi, in figura sono già stati assegnati i colori a tre segmenti. Di che colore può essere il segmento segnato con x ?

19In una stanza completamente buia, Simona prende a caso della frutta da un cesto che contiene 3 mele verdi, 5 mele gialle, 7 pere verdi e 2 pere gialle. Quanti frutti deve prendere Simona per essere sicura di avere almeno una mela e una pera dello stesso colore?

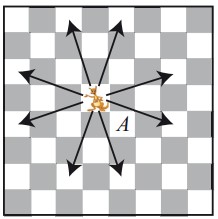
20In una nuova versione del gioco degli scacchi esiste anche un pezzo chiamato “Kang”. Le mosse che “Kang” può fare sono solo due: spostarsi di 3 caselle in verticale e di una 1 in orizzontale, oppure di 3 caselle in orizzontale e di una 1 in verticale, come mostrato in figura. Qual è il numero minimo di mosse che permette a “Kang” di passare dalla casella attuale a quella indicata con A?

21Nella somma qui indicata, lettere uguali rappresentano la stessa cifra, e lettere diverse cifre diverse. Quale cifra è rappresentata dalla lettera X ?

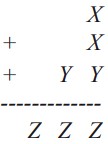
22Giovanna ha comprato 3 giocattoli. Per il primo ha pagato 1 euro più della metà dei soldi che aveva. Aggiungendo 2 euro a metà dei soldi che le erano rimasti ha comprato il secondo giocattolo e aggiungendo 3 euro alla metà di quello che le era rimasto dopo aver acquistato i primi due giocattoli ha comprato il terzo. In questo modo ha speso tutti i soldi che aveva. Quanti euro ha speso in tutto?

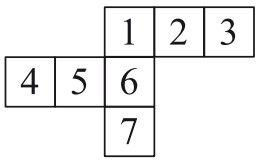
23Voglio rivestire di carta una scatola a forma di cubo, senza sovrapposizioni. Per questo ho disegnato su un foglio di carta e ritagliato la figura che vedi (composta da quadrati tutti uguali tra loro e uguali alle facce della scatola), che poi piegherò lungo ciascun lato comune a due quadrati. Per errore, però, ho disegnato 7 quadrati invece di 6. Devo quindi eliminarne uno, ma voglio che il foglio di carta non si spezzi in due e in particolare che non ci sia alcun quadrato unito solo per un vertice ad un altro. Quale quadrato posso eliminare?

24Aster deve indovinare un numero intero scritto da Laura. Laura dice che non ricorda bene come lo ha ottenuto: sa che è partita da 100, poi ha moltiplicato per 2 o per 3, ha aggiunto 1 o 2 e infine ha diviso per 3 o per 4. Qual è il numero scritto da Laura?

25ABCD è un numero di 4 cifre; le cifre A, B, C e D sono in ordine crescente da sinistra a destra. Considera i due numeri BD e AC: qual è il massimo valore possibile della differenza BD - AC ?

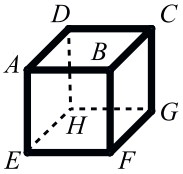
26Maria scrive un numero su ogni faccia del cubo in figura. Poi attribuisce ad ogni vertice del cubo la somma dei numeri scritti sulle 3 facce che contengono quel vertice (ad esempio, per il vertice B somma i numeri sulle facce BCDA, BAEF e BFGC). I numeri che Maria ottiene per i vertici C, D ed E sono rispettivamente 14, 16 e 24. Che numero ottiene per il vertice F ?

27Un treno ha 12 carrozze, ciascuna divisa in uno stesso numero di scompartimenti. Michele viaggia sulla terza carrozza, e, contando a partire dal primo dopo il locomotore, si trova nel 18-simo scompartimento. Sofia siede nella settima carrozza e, sempre contando a partire dal locomotore, il suo scompartimento è il 50-simo. Quanti scompartimenti ci sono in ogni carrozza?

28In quanti modi diversi si possono mettere i tre canguri nelle 7 caselle, non più di uno per casella, se non vogliamo avere 2 canguri in caselle adiacenti?

29Alberto ha segnato quattro punti distinti su una retta e ora, per ogni coppia di punti, misura la loro distanza. Dei sei numeri diversi fra loro che ottiene, cinque sono (elencati in ordine crescente): 2, 3, 11, 12, 14. Quello mancante è minore di 14. Qual è?

30Brando ha usato dei cubetti di lato 1 cm per costruire un cubo di lato 4 cm. Ha poi dipinto di rosso 3 facce del cubo grande e di blu le altre 3. Quando ha finito, si è accorto che nessuno dei cubetti piccoli aveva tre facce rosse. Quanti sono i cubetti che hanno sia facce rosse sia facce blu?