1Il popolo dei Maya scriveva i numeri non usando le nostre dieci cifre, ma solo due diversi simboli, punto e barra. Un punto valeva 1, una barra valeva come 5 punti e i numeri venivano scritti usando il minor numero possibile di simboli. Come scrivevano il numero 17?

2La somma dei punti che stanno su facce opposte di un dado regolare è sempre 7. Quale fra le seguenti può essere l’immagine di un dado regolare?

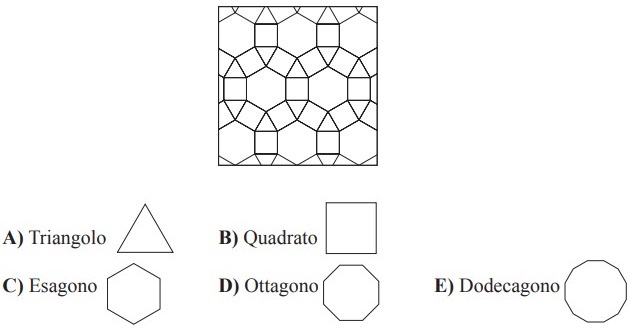
3I contorni delle figure che compongono il mosaico che ti mostriamo sono costituiti da segmenti rettilinei tutti della stessa lunghezza. Quale fra i seguenti poligoni regolari non compare nel mosaico?

4In una sala ci sono 14 donne e 12 uomini. Esattamente la metà di queste persone sono nate prima del 2000. Quante donne si può essere certi che siano nate prima del 2000?

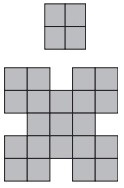
5Vuoi scegliere un quadrato 2 x 2 fra quelli che compaiono nella figura di sotto. In quanti modi diversi puoi farlo?

6Tina ha scattato in un certo ordine le quattro fotografie che vedi: esse mostrano lo stesso gruppo di persone che sono in cammino, nel verso dal basso delle foto verso l’alto. In quale ordine sono state scattate?

7Sulle facce di un dado, anziché i numeri da 1 a 6, compaiono i primi sei numeri interi dispari. Anna ha tirato il dado tre volte e ha sommato i tre punteggi ottenuti. Quale fra i seguenti sicuramente non è il risultato che ha ottenuto?

8Il giorno del gioco Kangourou è sempre il terzo giovedì di marzo: quest’anno corrisponde al giorno 21. E nel 2020 a quale giorno corrisponderà?

9La somma delle età in anni di un gruppo di canguri è 36. Fra due anni, la somma delle loro età sarà 60. Quanti sono i canguri in quel gruppo?

10In un giorno normale la gatta Lilli mangia 5 topi; se però è molto affamata, ne mangia 10. Negli ultimi 9 giorni ha mangiato in tutto 60 topi. In quanti giorni è stata molto affamata?

11Un orologio digitale segna le 20:19. Qual è l’ora più vicina alle 20:19, diversa dalle 20:19, che si scrive usando le stesse cifre?

12Usando alcuni cubi tutti uguali fra loro, Michele ha costruito i cinque solidi che vedi nelle figure e ora li vuole dipingere. Tutti hanno la base costituita da 8 cubi: qual è quello che richiede la maggiore quantità di vernice?

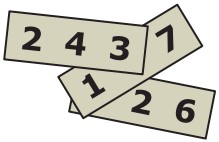
13In figura vedi tre targhette parzialmente sovrapposte. Su ognuna è scritto un numero di tre cifre: la somma dei tre numeri scritti è 826. Due delle nove cifre non sono visibili: qual è la loro somma?

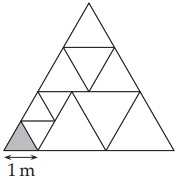
14Tutti i triangoli che si vedono in figura sono equilateri; il lato dei quattro più piccoli è lungo 1 metro. Quanti metri misura il perimetro del triangolo più grande?

15Nel giardino di una strega ci sono 30 animali: cani, gatti e topi. La strega trasforma 6 cani in altrettanti gatti, poi trasforma 5 gatti in altrettanti topi. A questo punto ci sono 10 cani, 10 gatti e 10 topi. Quanti gatti c’erano all’inizio?

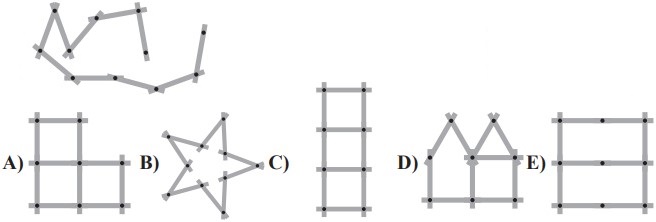
16In figura vedi un doppio-metro snodabile costituito da 10 segmenti di 20 centimetri ciascuno. Una sola delle cinque figure che vedi qui sotto non può essere formata con questo doppio-metro: quale?

17I cinque mosaici quadrati che vedi qui sotto hanno tutti la stessa dimensione. Ognuno è stato formato con tessere quadrate bianche o nere che, nei singoli mosaici, hanno tutte la stessa dimensione. In quale dei mosaici l’area della superficie nera è la più grande?

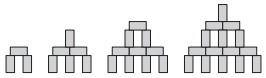
18Carlo ha 28 mattoncini, tutti lunghi 2 centimetri, larghi 1 e alti 1. Li vuole utilizzare tutti per costruire una torre: le figure ti mostrano con quale criterio Carlo intende portare avanti la sua costruzione. Quanti centimetri sarà alta la torre quando Carlo l’avrà ultimata?

19La figura ti mostra tre facce di un cubo, su ogni faccia del quale compare un numero intero maggiore di zero. Sai che il prodotto dei numeri che compaiono su facce opposte è lo stesso per le tre coppie di facce. Qual è il valore minimo possibile per la somma dei sei numeri?

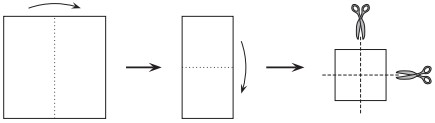
20La figura ti indica come Emanuele ha piegato due volte un foglio quadrato su sé stesso, in modo da ottenere alla fine ancora un quadrato. Poi ha tagliato il quadrato che ha ottenuto lungo due rette, ciascuna parallela a due lati. Quanti diversi pezzi di carta ha ottenuto?

21Aldo, Bruno e Carla hanno una bicicletta ciascuno. Si sa che, se Aldo non va in bicicletta, allora ci va Bruno; se Bruno non va in bicicletta, allora ci va Carla. Oggi Bruno non è andato in bicicletta. Chi è andato in bicicletta?

22Le due figure ti mostrano due bilance che sono in equilibrio grazie a due pesi, uno da 6 e l’altro da 30 grammi, aggiunti sui piatti a destra. Le biglie nere hanno tutte lo stesso peso, e così pure le tre biglie bianche (ovviamente diverso da quello delle biglie nere). Quanti grammi pesano le nove biglie tutte insieme?

23Papà Roberto ha fatto le seguenti cinque affermazioni. Una e una sola di esse è falsa. Quale?

24Beniamino ha scritto un numero intero maggiore di zero nel primo cerchio a sinistra nella figura; poi, eseguendo nell’ordine tutte le operazioni indicate, ha scritto i singoli risultati ottenuti nei cerchi successivi. Quanti dei sei numeri che ha scritto sono divisibili per 3?

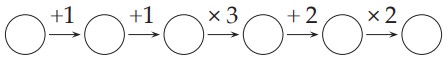
25Ognuna delle figure qui sotto mostra lo sviluppo di un cubo sulla cui superficie è stata tracciata una linea. Per uno solo degli sviluppi accade che, una volta ricostruito il cubo, la linea tracciata appare chiusa. Quale?

26Otto amici hanno scattato delle fotografie: in ognuna di esse compaiono cinque di loro, e ognuno di loro compare in almeno due ma non più di tre fotografie. Quante fotografie hanno scattato?

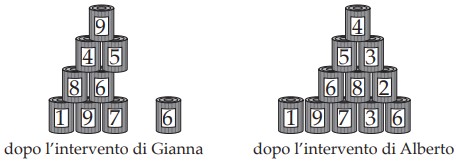
27Ci sono due piramidi costruite con delle lattine, su ognuna delle quali è riportato un punteggio. Le piramidi sono identiche, anche per quanto riguarda i punteggi e la loro disposizione. Gianna ha levato 6 lattine per un totale di 25 punti, Alberto ha levato 4 lattine: le figure ti mostrano che cosa è rimasto delle piramidi dopo ciascuno dei due interventi. Quanti punti ha totalizzato Alberto?

28Lina ha ottenuto un cubo accostando 64 cubetti tutti della stessa dimensione, 32 bianchi e 32 neri, e ha fatto in modo che la parte bianca della superficie del cubo grande sia la più estesa possibile. Che frazione della superficie del cubo grande appare bianca?

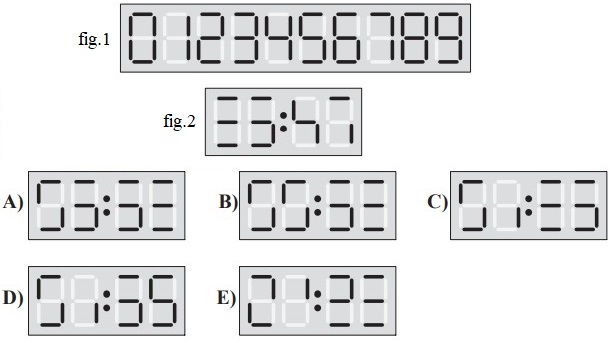
29Per fare apparire ciascuna cifra del mio orologio digitale occorre illuminare al più sette segmenti. Ecco come devono apparire le dieci cifre (fig.1). Sfortunatamente, in ognuna delle quattro posizioni (ore e minuti) ci sono due segmenti che non si illuminano mai, gli stessi due per tutte le posizioni. Ecco quello che sto vedendo ora sul mio orologio (fig.2). Che cosa vedrò fra 3 ore e 45 minuti?

30Filippo gioca con due macchine cambia-gettoni: una dà quattro gettoni rossi per uno bianco, l’altra dà tre gettoni bianchi per uno rosso. Inserendo un gettone alla volta in una delle due macchine e potendole usare entrambe, dopo aver giocato 10 volte Filippo si ritrova con 28 gettoni. Sapendo che, prima di giocare, aveva 4 gettoni bianchi, quanti gettoni rossi ha ora?