1Quale tra i parallelepipedi mostrati nelle risposte si può comporre utilizzando questi sei mattoni, identici per dimensioni?

2In questa immagine tutti i bambini si tengono per mano. Quante volte succede che entrambe le mani che si stringono siano mani sinistre?

3Incastrando le cinque tessere del puzzle in modo corretto si ottiene un rettangolo in cui si legge un’addizione. Qual è il risultato?

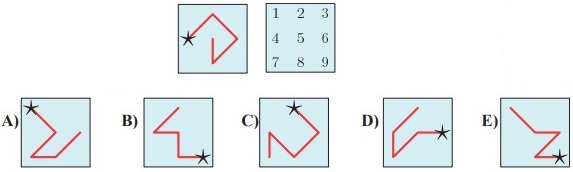
4In figura vedi come Lisa ha inserito in un quadrato le cifre da 1 a 9. Lisa gioca così: disegna un percorso che congiunge alcune cifre e poi compone il numero che ottiene trascrivendo nell’ordine le cifre che incontra sul percorso, a partire da quella che ha denotato con una stella. Ad esempio, con il percorso a sinistra, scriverebbe il numero 42685. Quale dei seguenti percorsi permette a Lisa di scrivere il numero maggiore?

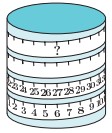
5Un metro a nastro è avvolto attorno a un cilindro come mostra la figura. Quale numero si ritrova in corrispondenza della tacca indicata dal punto di domanda?

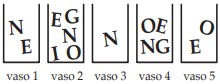
6Sofia vuole scrivere la parola GENIO estraendo una lettera da ciascuno di questi cinque vasi. Quale lettera deve estrarre dal vaso 4?

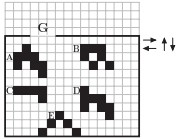
7Supponi di poter traslare (anche più volte) una figura disegnata su un foglio a quadretti ma solo nelle direzioni indicate dalle 4 frecce. Quale delle cinque figure nel disegno può, in assenza delle altre, uscire dal rettangolo attraverso l’apertura G?

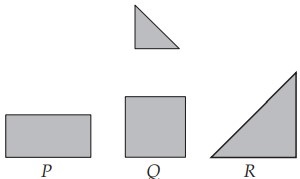
8Maria aveva un foglio di carta. L’ha piegato esattamente a metà e poi l’ha piegato nuovamente a metà e ha ottenuto la figura. Tra le forme P, Q e R che vedi sotto, quale potrebbe essere stata quella del foglio di carta originario?

9In una cassetta c’erano 20 mele e 20 pere. Carlo ha preso a caso 20 frutti dalla cassetta e Luca ha preso tutti quelli restanti. Quale delle seguenti affermazioni è sicuramente vera?

10In un quadrato Dani ha tracciato dei segmenti aventi per estremi un vertice del quadrato o punti medi dei suoi lati o di altri segmenti precedentemente individuati. Poi ha colorato una delle figure delimitate dai segmenti e ha osservato che ha colorato 1/8 del quadrato grande. Qual è il disegno di Dani?

11Giulio ha scritto il numero 5021972970 su una striscia di carta; poi ha tagliato la striscia in due punti; ha così ottenuto tre numeri che poi è andato a sommare. Qual è la somma più piccola che Giulio può aver ottenuto?

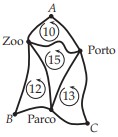
12La mappa mostra i capolinea A, B, C di tre linee circolari di autobus e alcuni luoghi che esse collegano. 1)Il percorso capolinea A - zoo - porto - capolinea A è lungo 10 km; 2)Il percorso capolinea B - parco - zoo - capolinea B è lungo 12 km; 3)Il percorso capolinea C - porto - parco - capolinea C è lungo 13 km; 4)Il percorso misto sulle tre linee: zoo - parco - porto - zoo è lungo 15 km. Quanti chilometri è lungo il percorso circolare lungo la strada più esterna rappresentata nella mappa?

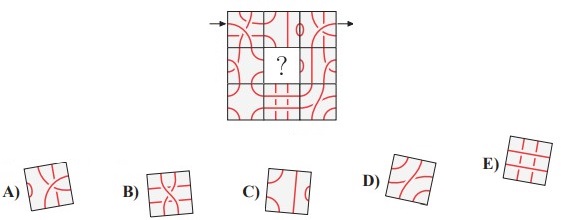
13Rosa percorre il labirinto in figura entrando dal punto indicato dalla freccia a sinistra ed uscendo dal punto indicato dalla freccia a destra. Quale delle seguenti tessere non può stare al centro della figura?

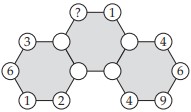
14In alcuni vertici dei tre esagoni in figura sono stati inseriti dei numeri. Vogliamo inserire dei numeri anche nei restanti vertici in modo che la somma dei sei numeri che circondano ciascun esagono sia 30. Che numero si deve inserire nel vertice denotato con il punto di domanda?

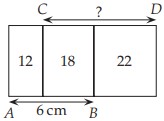
15Tre rettangoli con la stessa altezza sono accostati come mostra la figura. I numeri scritti all’interno dei rettangoli denotano le loro aree in centimetri quadrati. Se il segmento AB è lungo 6 cm, quanti centimetri è lungo il segmento CD ?

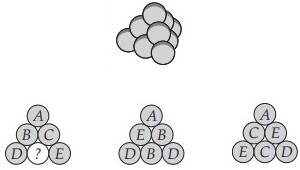
16Ho costruito una piramide a base triangolare sovrapponendo 10 sfere di misure identiche. Ogni sfera è colorata con uno solo tra cinque colori che denotiamo con le lettere A, B, C, D, E; hanno uno stesso colore esattamente due sfere. L’immagine che segue mostra tre facce laterali della piramide: di quale colore è la sfera con il punto di domanda?

17Roberto ha quattro gettoni bianchi e Vittorio ne ha quattro grigi. Essi a turno dispongono uno dei loro gettoni in modo da formare due pile di ugual altezza. Roberto inizia il gioco. Quale delle cinque coppie di pile che vedi qui sotto non può essere realizzata?

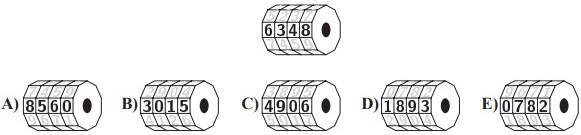
18Per la bici ho un lucchetto a combinazione composto da quattro ghiere, ciascuna delle quali riporta nell’ordine le cifre da 0 a 9, come si intuisce dalle figure. Per gioco, dopo che avevo inserito la combinazione corretta, il mio fratellino ha girato ogni ghiera nello stesso verso e dello stesso numero di scatti. Adesso il lucchetto mostra la combinazione 6348. Quale delle seguenti non può essere la combinazione corretta del mio lucchetto?

19Carla vuol dipingere di verde le pareti della sua stanza. La tempera verde comperata in negozio è troppo scura, quindi pensa di mescolarla con tempera bianca. Fa diverse miscele di prova: quale delle seguenti darà il colore verde meno scuro?

20La linea ferroviaria che unisce X e Y è a doppio binario. I treni vi viaggiano a velocità costante. Per percorrerla, un treno merci impiega 180 minuti, un treno rapido impiega 60 minuti. Se nello stesso istante un treno merci parte da X e un treno rapido da Y, in quale tratto si incroceranno?

21Anna, Bob, Cecilia, Dani ed Eva sono seduti attorno a un tavolo rotondo. Anna non è vicina a Bob, Dani è vicino a Eva. Quali sono le due persone che siedono vicino a Cecilia?

22Maurizio ha chiesto al capo pasticciere la ricetta dei pancakes. Gli ingredienti per 100 pancakes sono: 25 uova, 4 l di latte, 5 kg di farina, 1 kg di burro. Maurizio ha 6 uova, 400 g di farina, 0,5 litri di latte e 200 g di burro. Usando questa ricetta, qual è il massimo numero di pancakes che Maurizio riuscirà a fare?

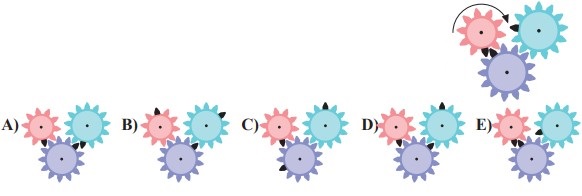
23La figura mostra un ingranaggio costituito da tre ruote dentate, ciascuna con un dente nero. Quale delle figure nelle risposte mostra la posizione corretta dei denti neri dopo che la ruota piccola ha fatto un intero giro in verso orario?

24Peso a coppie quattro frutti. La mela e l’arancia pesano quanto la pera e la pesca. La mela e la pera pesano meno dell’arancia con la pesca. La pera e l’arancia pesano meno della mela con la pesca. Quale frutto è il più pesante?

25Vogliamo aggiungere al disegno dei quadretti colorati in modo da realizzare una figura simmetrica rispetto a ciascuno dei quattro assi di simmetria della griglia. Qual è il minimo numero di quadretti che permette di farlo?

26Alle due domande “Quanti dobloni e quanti diamanti ha il tuo amico Barbanera?” tre pirati hanno dato, ciascuno, una risposta vera e una falsa. Le loro risposte sono state: (1) Ha 8 dobloni e 6 diamanti. (2) Ha 7 dobloni e 4 diamanti. (3) Ha 7 dobloni e 7 diamanti. Qual è la somma del numero di dobloni e del numero di diamanti posseduti da Barbanera?

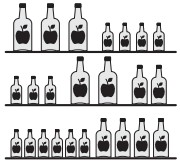
27Guarda la figura: su ognuno dei tre scaffali ci sono in tutto 64 decilitri di succo di mela. Le bottiglie hanno tre misure diverse: grande, media e piccola. Quanti decilitri di succo di mela contiene la bottiglia media?

28Un cubo ha spigolo lungo 7 cm ed è composto da tanti cubetti con spigolo lungo 1 cm incollati tra loro. Su ciascuna delle facce del cubo più grande sono state tracciate le due diagonali con un pennarello rosso. Quanti dei cubetti hanno almeno una faccia su cui compare almeno una riga rossa?

29Lucia trasforma i numeri da 1 a 100 seguendo questa regola: a ogni numero N sostituisce il numero che si ottiene sommando a N la somma delle sue cifre. Tra i numeri così ottenuti, quanti sono pari?

30Un gruppo di 10 tra fate e streghe partecipa a una festa: a ciascuna di esse viene dato un biglietto su cui è stampato un numero da 1 a 10 e non ci sono due partecipanti con lo stesso numero. È noto che le fate dicono sempre la verità, mentre le streghe possono anche mentire. A ciascuna viene chiesto di dire il numero stampato sul proprio biglietto e ciascuna di esse risponde con un numero compreso tra 1 e 10. La somma dei numeri pronunciati è 36. Qual è il minimo numero possibile di streghe presenti alla festa?