1Lancio simultaneamente tre dadi e sommo i punti che appaino sulle loro facce superiori. Quanti sono i diversi valori possibili di tale somma?

2Gli studenti A, B, C, D, E ed F sono disposti in fila indiana. Si sa che: 1) D si trova tra E ed F; 2) C tra D ed E; 3) B tra C e D; 4) A tra B e C. Quale delle seguenti affermazioni è vera?

3Una delle diagonali d divide un poligono di perimetro 31 cm in due poligoni di perimetro rispettivamente 21 cm e 30 cm. Allora la lunghezza di d è

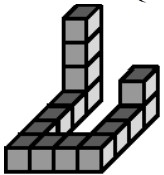
4Il solido rappresentato nella figura è formato da cubetti di lato unitario. Qual è il minimo numero di cubetti di lato unitario che occorre aggiungere per formare un cubo che contenga il solido iniziale? (I cubetti esistenti non possono essere spostati).

5m è un intero positivo tale che MCD (m, 35) > 10. Quale delle seguenti affermazioni è certamente vera? Nota: MCD (a, b) indica il massimo comune divisore tra a e b.

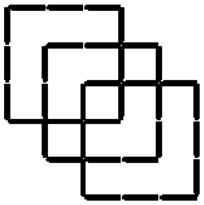
6Trova il minimo numero di fiammiferi che bisogna aggiungere alla figura in modo da ottenere esattamente 11 quadrati.

7Quanti sono i numeri primi minori di 2001 la somma delle cui cifre è uguale a 2?

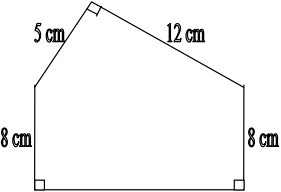
8Il perimetro del poligono raffigurato (i tre angoli indicati sono retti) vale

9Quante cifre contiene la rappresentazione decimale del più piccolo intero positivo che può essere scritto usando le sole cifre 0 e 1, e che sia divisibile per 225?

10Tagliando un solo anello, è possibile liberarli tutti?

11a, b, c e d sono interi positivi tali che a + b = c d e che a + b + c = 12. Quanti sono i possibili diversi valori che può assumere d ?

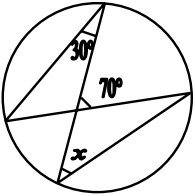
12Qual è la misura dell'angolo “x” nella figura?

13Un orologio ritarda di X minuti ogni Y ore. Quante ore, in termini di X e Y, ritarderà quell'orologio in una settimana?

14Gaspare aveva 400 franchi e doveva acquistare 100 tavolette di cioccolato al costo di 4 franchi l'una. Nel supermercato ha scoperto che per ogni 6 tavolette di cioccolato che aveva nel carrello, una nuova tavoletta veniva aggiunta gratuitamente alla cassa. Quanti franchi sono rimasti a Gaspare all'uscita dal supermercato, sapendo che oltre al cioccolato non ha acquistato altro?

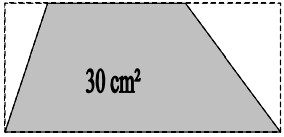
15Due triangoli sono stati tolti da un rettangolo (si veda la figura). Il restante trapezio ha l'area di 30 cm² e la sua base maggiore è doppia della minore. Qual è la somma delle aree dei due triangoli che sono stati tolti?

16Ogni volta che il cammello Desirée ha sete, l'84% del suo corpo è costituito da acqua. Dopo aver bevuto, il suo peso raggiunge gli 800 kg e l'acqua costituisce l'85% del suo peso. Qual è il peso del cammello Desirée quando ha sete?

17Il prodotto delle età dei miei figli (in anni) è 1664. Il più giovane ha la metà degli anni del più anziano e non vi sono gemelli. Quanti figli ho?

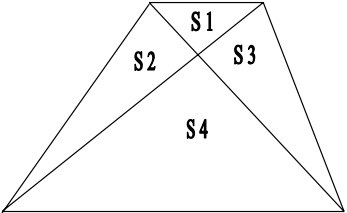
18Il trapezio ABCD è suddiviso dalle sue diagonali in quattro triangoli di area S 1, S2, S 3, S 4 (si veda la figura). Se S 2 = 3 ⋅ S 1, allora

19Nell'espressione 2 * 4 * 6 * 8 * 10 * 12 * 14 ad ogni asterisco può essere sostituito il segno “ + ” o il segno “ – ”. Quale numero non può essere il risultato di alcuna di queste espressioni ?

20Nella divisione 999 : n, dove n è un numero naturale di due cifre (significative), il resto vale 3. Allora il resto della divisione 2001 : n vale

21In una scatola di caramelle vi erano 31 caramelle. Il primo giorno Cristina mangiò i 3/4 del totale delle caramelle che Paolo aveva appena mangiato prelevandole da quella scatola. Il secondo giorno Cristina mangiò i 2/3 del totale delle caramelle appena mangiate da Paolo nel secondo giorno (sempre prelevate dalla stessa scatola). Alla fine del secondo giorno la scatola era vuota. Quante caramelle ha mangiato Cristina da quella scatola?

22Un triangolo rettangolo ABC come in figura, con AB = c, AX = p e XC = q, rappresenta un terreno. Jenny e Vicky camminano alla stessa velocità in direzioni opposte sul bordo del erreno, partendo entrambe allo stesso istante dalla posizione X. Le due ragazze si incontrano in B. Qual è il valore di q in funzione di p e c?

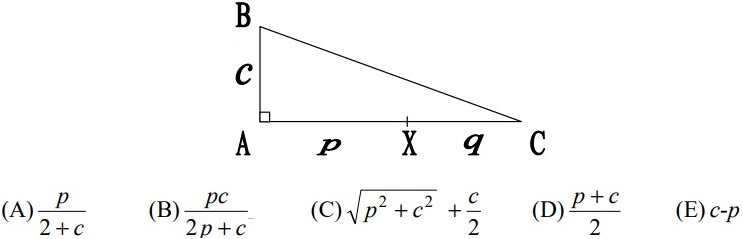
23Ho 11 scatole grandi: alcune di esse contengono 8 scatole medie ciascuna, alcune delle scatole medie contengono a loro volta 8 scatole piccole ciascuna. Se le scatole (di varia dimensione) vuote sono 102, quante sono in totale le scatole (a prescindere dalla dimensione)?

24Sia a = 1997¹⁹⁹⁸ + 1998¹⁹⁹⁹ + 1999²⁰⁰⁰ + 2000²⁰⁰¹. La cifra delle unità di a è

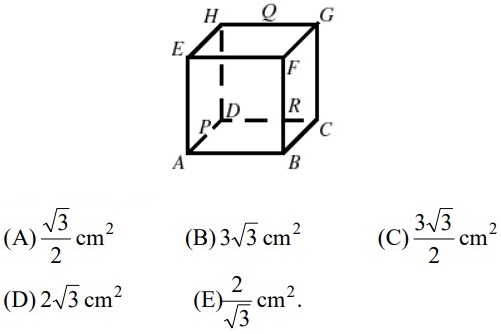
25ABCDEFGH è un cubo di lato 2 cm. P, Q e R sono i punti medi di AD, GH e BF rispettivamente. Quanto misura l'area del triangolo PQR?

26Nella griglia, la distanza tra due punti adiacenti è 1 cm sia in orizzontale sia in verticale. Congiungete due punti in modo da formare un segmento lungo 5 cm. Quanti di questi segmenti possono essere tracciati nella griglia?

27Cancelliamo la cifra delle unità di un intero positivo e notiamo che il numero diminuisce di 14 volte. Quanti numeri interi possiedono questa proprietà?

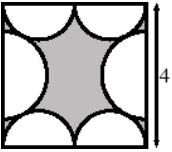
28Se A è l'area del quadrato (di lato 4) e B è l'area totale dei sei semicerchi come in figura, allora il valore di A – B è

29In quanti modi differenti si può piastrellare un pavimento di forma rettangolare di dimensione 2 × 8, utilizzando delle piastrelle rettangolari di dimensione 1 × 2 (senza sovrapposizioni)?

30In quanti modi differenti si può scomporre il numero 30 come somma di tre interi strettamente positivi? (Due scomposizioni sono uguali se differiscono solo per l'ordine degli addendi.)