1Giuseppe ha 100 topolini ognuno dei quali è o bianco o grigio. Comunque si scelga un gruppo di sette topolini, almeno quattro sono bianchi. Qual è il massimo numero di topolini grigi che Giuseppe può avere?

2Qual è il massimo numero di palline di legno di raggio 1 cm che e’ possibile inserire in una scatola di forma cubica di volume 64 cm³ ?

3Se log₂ 10 = a allora log₁₀ 2 vale

4Quanti sono i numeri interi positivi non primi minori di 1000 la somma delle cui cifre (in rappresentazione decimale) valga 2?

5Qual è la probabilità che, scegliendo a caso un numero di 3 cifre (significative), esso sia pari e maggiore di 399?

6Risolvi:

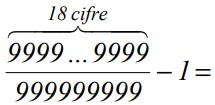
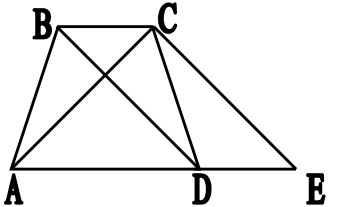
7Nella figura BC è parallelo ad AE e BD è parallelo a CE. Se x è l'area del quadrilatero ABCD e y l'area del triangolo ACE, allora

8Il numero delle diverse quaterne di interi positivi (x, y, z, t) tali che x < y < z < t e xyzt - 1 = 2001, è uguale a

9Due ciclisti partono dallo stesso punto alle 14.10. Il primo va verso nord ad una velocità di 32 km/h, mentre il secondo va verso est ad una velocità di 24 km/h. La distanza fra loro sarà di 130 km alle

10m è un intero positivo tale che MCD (m, 35) > 10. Quale delle seguenti affermazioni è certamente vera? Nota: MCD (a, b) indica il massimo comune divisore tra a e b.

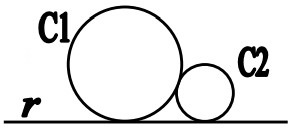
11Due circonferenze C1 e C2 di raggio diverso sono tangenti esternamente e tangono entrambe la stessa retta r (v. figura). Quale delle seguenti affermazioni è vera?

12La figura mostra lo sviluppo piano di un solido delimitato da tre quadrati di lato 4 cm e due triangoli equilateri. Qual è il volume del solido?

13A New York 16 pacchetti di gomma da masticare costano tanti dollari quanti sono i pacchetti che si riescono a comperare con un dollaro. Quanti centesimi costa un pacchetto? (1 dollaro = 100 centesimi).

14Sia 1, 4, 9, 16, … la successione dei quadrati dei numeri naturali. Il numero 10 8 è un termine di questa successione. Quale dei seguenti numeri è il termine successivo della successione?

15ABCDEF è un esagono regolare. Allora il vettore (fig.1) coincide con il vettore (fig.2):

16In un torneo fra 4 squadre di calcio (ogni squadra ha giocato contro ogni altra squadra una ed una sola volta), la classifica finale è la seguente: squadra A 7 punti, squadra B 4 punti, squadra C 3 punti, squadra D 3 punti. (Nelle partite di calcio una squadra ottiene 3 punti quando vince, 1 punto quando pareggia, 0 punti in caso di sconfitta). Come è finito l'incontro tra la squadra A e la D?

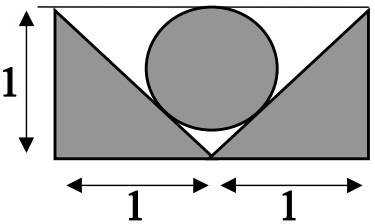
17Quanto vale l'area della figura in grigio, formata da due triangoli e da un cerchio?

18L'ipotenusa di un triangolo rettangolo è lunga 0,9 cm mentre le lunghezze dei cateti sono a cm e b cm. Qual è il più piccolo tra i seguenti numeri?

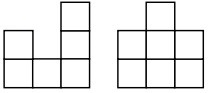
19Nella figura avete la vista da sinistra e frontale di una costruzione ottenuta accostando piccoli cubi. Quanti cubetti sono stati usati? Vengono richiesti il numero minimo ed il numero massimo di cubetti compatibili con le raffigurazioni mostrate.

20Un triangolo equilatero CDE viene costruito esternamente ad un quadrato ABCD sul lato CD. Quanti gradi misura l'angolo AEC?

21Trova la lunghezza del lato maggiore del rettangolo presentato nella figura (il lato minore misura 1), sapendo che le figure rotonde sono tutte cerchi.

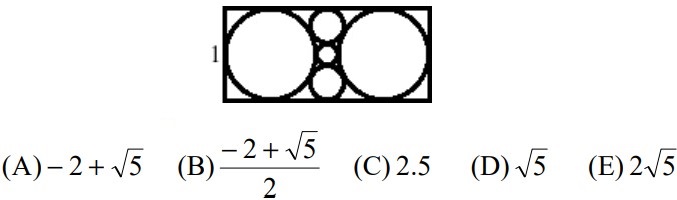
22Le celle di una griglia di 43 righe × 43 colonne sono colorate con 4 colori 1, 2, 3, 4 come mostrato nella figura. Quale colore è usato più spesso rispetto ad ognuno degli altri tre?

23Per ogni numero intero positivo n calcoliamo la somma delle sue cifre (in rappresentazione decimale), poi la somma delle cifre del numero ottenuto e così via, fino ad ottenere un numero di una sola cifra che viene denotato con w(n). Il numero w(2001²⁰⁰¹) è uguale a

24Quante fra le coppie di cifre 00, 11, 22, 33, 44, 55, 66, 77, 88, 99 possono essere la coppia delle ultime due cifre del quadrato perfetto di un numero intero?

25Siano m e n due numeri interi positivi tali che log₁₀ m = 12.3… e log₁₀ n = 15.4…. Quante cifre ha il prodotto m ⋅ n?

26Due uomini e due ragazzi vogliono attraversare un fiume usando una piccola canoa che può portare al massimo o due ragazzi o solo un adulto. Qual è il minimo numero di traversate necessario per trasportare dall'altra parte del fiume tutte le persone?

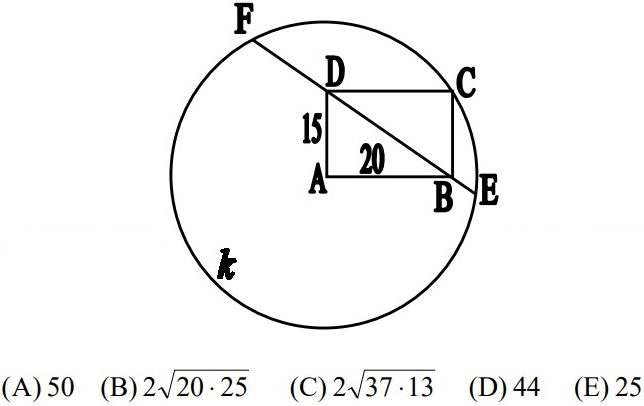
27Se ABCD è un rettangolo e k è una circonferenza con centro in A e passante per C, qual è la lunghezza della corda EF? (vedi figura).

28Sommando numeratore e denominatore, quando essi siano ridotti ai minimi termini, del risultato della seguente espressione, si ottiene:

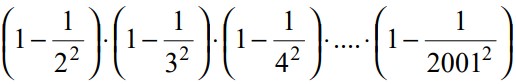
29Lo zio Marco ha pescato alcuni pesci. Dà i tre più grandi al suo cane, riducendo il peso totale della sua pesca del 35%. Dà poi i tre pesci più piccoli al suo gatto, riducendo il peso totale rimanente dei 5 / 13. La famiglia mangia i restanti pesci per cena. Quanti pesci ha catturato lo zio Marco?

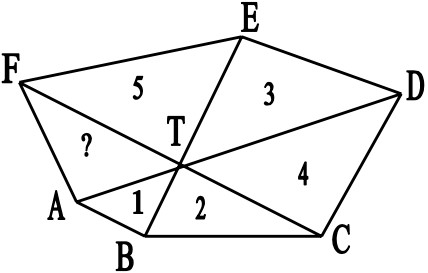
30Le diagonali AD, BE, CF di un esagono convesso ABCDEF passano tutte per uno stesso punto T. Quanto vale l’area del triangolo FAT, se le aree degli altri sono quelle indicate in figura?