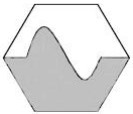
1La figura rappresenta un esagono regolare suddiviso in due regioni. Quanto vale il rapporto fra il perimetro della regione ombreggiata e quello della regione complementare?

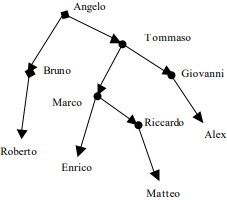
2Matteo esamina il proprio albero genealogico dove sono riportati solo i maschi e dove le frecce indicano il verso dal padre ai rispettivi figli. Qual è il nome del figlio del fratello del nonno del fratello del padre di Matteo?

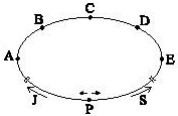
3Jack corre ad una velocità che è il triplo di quella della sua sorellina Susanna. Essi partono nello stesso istante dallo stesso punto P della pista rappresentata in figura, movendosi in direzioni opposte e seguendo la pista. In quale punto si incontreranno per la prima volta?

4Sei bambini hanno mangiato insieme complessivamente 20 biscotti. Andrea ne ha mangiato uno, Beatrice due e Carlo tre. Daniela ha mangiato più biscotti di ognuno degli altri bambini. Qual è il più piccolo numero di biscotti che può aver mangiato Daniela?

5Sia l la lunghezza della più lunga linea spezzata, formata da segmenti aventi gli estremi nei vertici di un quadrato di lato 1, che è possibile tracciare senza mai staccare la penna dal foglio e senza percorrere due volte alcun segmento (è ammesso passare più di una volta per qualche vertice). Qual è, fra i seguenti numeri, quello più vicino a l?

6Quanto vale la differenza tra il più grande ed il più piccolo numero intero positivo, ciascuno formato da esattamente 3 cifre significative a due a due diverse fra loro?

7Qual è il più piccolo numero di facce che può avere un poliedro, una faccia del quale sia un pentagono?

8Un numero intero si dice “primo” se è maggiore o uguale a 2 e se ammette come divisori interi positivi solo 1 e sé stesso (esistono infiniti numeri primi). Con quanti zeri termina la rappresentazione decimale del prodotto dei primi 2002 numeri primi?

9Un computer è affetto da un virus che, nel corso del giorno in cui è stato inoculato, ne ha danneggiato la metà del disco fisso. Durante il giorno successivo il virus ha danneggiato 1/3 della parte di disco rimanente; durante il terzo giorno il virus ha danneggiato 1/4 della parte ancora sana all’inizio del giorno e durante il quarto giorno 1/5 della parte ancora sana all’inizio del giorno. A questo punto, quale frazione del disco fisso è rimasta sana?

10Alberto mente sempre. Un giorno disse al suo vicino Franco: “Almeno uno di noi non mente mai”. Sulla base di queste informazioni si può essere certi che

11Quanto vale S?

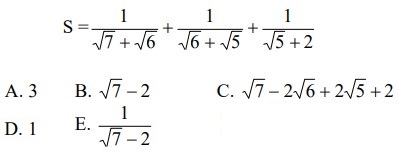
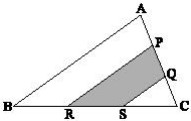
12Il triangolo ABC in figura ha area 1. I punti P e Q sul lato AC sono disposti in modo che i segmenti AP, PQ e QC abbiano la stessa lunghezza; i punti R e S sul lato BC in modo che i segmenti BR, RS e SC abbiano la stessa lunghezza. Qual è l'area della regione ombreggiata?

13Un canguro fenomenale si sposta saltando in linea retta da Trieste a Mosca (le due città distano circa 2 500 Km) e ogni salto è lungo il doppio del salto precedente. Se il primo salto è lungo 1 metro, dopo quanti salti il canguro sarà il più vicino possibile a Mosca?

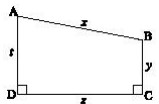
14Un trapezio ABCD rettangolo in D e C, avente base maggiore AD, ha il perimetro lungo 16. Se le lunghezze dei lati sono tutte espresse da numeri interi, quanto è lungo il lato BC?

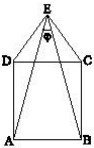
15Osservate la figura: ABCD è un quadrato, mentre CDE è un triangolo equilatero. Quanto misura in gradi l'angolo φ?

16Da un gruppo formato da ragazzi e ragazze se ne vanno 15 ragazze: a questo punto per ogni ragazza che rimane vi sono esattamente 2 ragazzi. Dopo un po’ abbandonano il gruppo 45 ragazzi: ora per ogni ragazzo che rimane sono presenti 5 ragazze.. Quante ragazze c’erano originariamente nel gruppo?

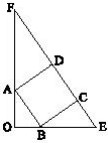
17Osservate la figura: OEF è un triangolo rettangolo, ABCD è un quadrato, il segmento OA è lungo 48 mentre il segmento OB è lungo 36. Quanto è lungo il segmento EF ?

18Un ciclista e un podista si muovono su un circuito circolare lungo 550 metri con velocità costanti di 10 m/s il ciclista, di 1 m/s il podista. Partono in versi opposti da uno stesso punto del circuito: quando si incontrano il ciclista prosegue la sua corsa, mentre il podista immediatamente si volta e si mette ad inseguire il ciclista. Con quanti secondi di ritardo rispetto al ciclista il podista avrà raggiunto il punto di partenza?

19Assegnato un numero reale x qualunque, un robot ha le sole possibilità di trasformarlo nel numero x + 3 o nel numero x - 2 o nel numero 1 / x o nel numero x² . Gli è concesso di eseguire la trasformazione per 3 volte consecutive, con piena libertà di scelta ad ogni passo. Inizialmente gli viene assegnato il numero 1,99. Se indichiamo con y il più grande numero che il robot può ottenere alla fine, allora

20Il signor Rossi impiega 90 secondi per portarsi al sesto piano di un grande magazzino salendo a piedi i gradini di una scala mobile quando questa non è in funzione; ne impiega invece 60 quando la scala è in funzione, ma si lascia trasportare senza muoversi. Quanti secondi impiega se la scala è in funzione e contemporaneamente egli ne sale i gradini?

21Le misure in centimetri dei lati di un rettangolo sono numeri interi e il suo perimetro vale 32. Quale, tra i seguenti numeri, può coincidere con la sua area (in cm² )?

22Dobbiamo trasportare contemporaneamente 50 scatole usando autocarri della portata di 1200 kg ciascuno. La prima pesa 150 kg, la seconda 151 kg, la terza 152 kg e così via fino all’ultima che pesa dunque 199 kg. Qual è il minimo numero di autocarri sufficiente ad effettuare il trasporto?

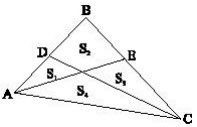
23Assegnato un triangolo ABC, lo si suddivida in 4 poligoni S1, S2, S3, S4 scegliendo due punti D e E, rispettivamente sul lato AB e sul lato BC, come mostrato nella figura. È possibile scegliere D e E in m modo che i 4 poligoni abbiano la stessa area?

24Lo sfruttamento medio della capacità ricettiva di un albergo è 88 % durante i tre mesi estivi e 44 % durante i rimanenti mesi dell’anno. Qual è lo sfruttamento medio relativo all'intero anno?

25Un terremoto ha danneggiato il quadrante dell'orologio della torre, che ha forma circolare. Sorprendentemente le lancette sono riamaste intatte e ora sono disposte lungo due segmenti rettilinei, uno congiungente il numero undici con il numero tre e l'altro il numero uno con il numero otto. Quanto è ampio (in gradi) il più piccolo fra i due angoli che essi determinano?

26Le lunghezze degli spigoli di una piramide a base triangolare ABCD sono: AB = 9, BC = 12, CA = 8, AD = 6, BD = 12 e CD = 4. Quante coppie di triangoli simili distinti si possono individuare tra le facce della piramide?

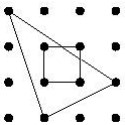
27Nella figura, due punti comunque scelti, purché adiacenti in orizzontale o in verticale, distano 1 metro. Quanto vale (in metri quadrati) l'area della parte comune al triangolo e al quadrato indicati?

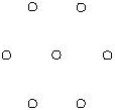
28Diciamo che tre punti non allineati formano una “V con vertice assegnato” se uno di essi (il vertice, appunto) è equidistante dagli altri due. Quante “V con vertice assegnato” si riescono ad individuare in un insieme di 7 punti, 6 dei quali siano i vertici di un esagono regolare e il settimo sia il centro dello stesso esagono?

29Quanto vale la somma 2 · 2² + 3 · 2³ + 4 · 2⁴ + … + 10 · 2¹⁰ ?

30Quanti numeri interi di 4 cifre significative sono tali che la somma delle ultime due cifre e del numero formato dalle prime due coincida con il numero formato dalle ultime due cifre? (Un numero che soddisfa la condizione descritta è, ad esempio, 6370: infatti 7 + 0 + 63 = 70.)