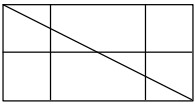
1Quanti triangoli si possono individuare nella figura?

2Per ogni intero positivo n, indichiamo con n! il prodotto di tutti gli interi positivi minori o uguali a n, ciascuno preso una sola volta (per esempio si ha 4! = 24). Determinate l’ultima cifra (della rappresentazione decimale) del numero 1! + 2! + 3! + … + 2002!

3Quanti sono i numeri interi positivi la cui rappresentazione decimale è costituita da tre cifre significative due almeno delle quali siano uguali?

4Siano a e b due interi positivi il cui Massimo Comune Divisore è 3. Sapendo che il quoziente a/b vale 4/10, quanto vale il prodotto a·b?

5Un prisma ha 2002 vertici. Qual è il numero dei suoi spigoli?

6Quando viene congelata, l’acqua aumenta di 1/11 il proprio volume. Di quanto diminuisce il volume del ghiaccio quando, fondendo, ritorna acqua?

7Lo sfruttamento medio della capacità ricettiva di un albergo è 88% durante i tre mesi estivi e 44% durante i rimanenti mesi dell'anno. Qual è lo sfruttamento medio relativo all'intero anno?

8Un bicchiere cilindrico di base a parzialmente pieno di acqua e inclinato di 45° si presenta come mostrato in figura. Quale percentuale del bicchiere contiene acqua?

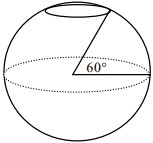
9La lunghezza dell'equatore è di circa 40 000 km. La lunghezza del parallelo che si trovi a 60° di latitudine Nord (si veda la figura), arrotondata alle centinaia di km è

10L'alfabeto del popolo marziano dei Berals è formato dalle sei lettere A, B, E, L, R, S prese in questo ordine. Le parole del loro linguaggio sono esattamente le sequenze, ordinate alfabeticamente, di queste sei lettere, dove ogni lettera viene utilizzata una e una sola volta. Qual è la parola che si trova alla 537-sima posizione del loro dizionario?

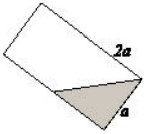
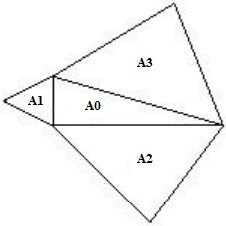
11La figura mostra 4 triangoli aventi aree Aᵢ (i = 0, 1, 2, 3). Il triangolo di area A₀ è rettangolo, gli altri tre sono equilateri. Allora necessariamente:

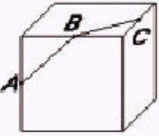
12La scultura astratta che si vede nella figura è stata ottenuta asportando un parallelepipedo rettangolo da un solido che originariamente era un cubo. Il volume del cubo originale era di 512 dm3 . Qual è l'area della superficie totale della scultura?

13Ad una gara di pesca sono presenti Pietro con suo figlio e Giovanni con suo figlio. Pietro ha preso tanti pesci quanti ne ha preso suo figlio. Giovanni invece ha pescato il triplo del numero dei pesci di suo figlio. Insieme hanno pescato 35 pesci. Il figlio di Pietro si chiama Luca. Come si chiama il figlio di Giovanni?

14Dieci squadre partecipano ad un torneo di calcio (ogni squadra gioca contro tutte le altre una e una sola volta). Al termine di ogni partita alla squadra vincente vanno 3 punti e alla perdente 0, in caso di pareggio si assegna 1 punto ad entrambe le squadre. Sommando i punti totalizzati dalle dieci squadre si ottiene 130. Quanti incontri sono terminati in pareggio?

15Apportando una modifica ad un impianto, in un processo industriale, è possibile ridurre le spese di produzione del 50 %; una diversa modifica le può ridurre del 40 %, mentre una terza modifica consente una riduzione del 10 %. Di quale percentuale sarebbero ridotte le spese di produzione se introducessimo simultaneamente le 3 modifiche che sono fra loro indipendenti?

16Quanto misura l'angolo formato dai segmenti AB e BC, sapendo che A, B e C sono i punti medi degli spigoli del cubo?

17Alcuni oggetti di quattro tipi, A, B, C, D, disposti su tre bilance come in figura, le fanno stare in equilibrio. Quanti oggetti del tipo C bilanciano un oggetto del tipo B ?

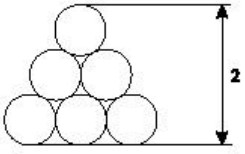
18Il “triangolo” nella figura a lato è formato da cerchi dello stesso raggio r. L'altezza del “triangolo” è 2. Quanto misura il raggio r ?

19Achille piè veloce insegue la tartaruga che cammina lentamente davanti a lui. La distanza iniziale tra loro è di 990 metri. La velocità di Achille è di 10 metri al secondo, la velocità della tartaruga è di 1 metro ogni 10 secondi. Dopo quanto tempo Achille raggiungerà la tartaruga?

20In una sequenza di numeri razionali positivi, ogni termine esclusi i primi due è la somma di tutti quelli che lo precedono. L'undicesimo termine della successione è 1000 ed il primo è 1. Qual è il secondo termine?

21Sono dati esattamente dieci punti nel piano. Cinque di questi stanno su una retta e nessuna altra retta contiene più di due punti tra quelli dati. Quanti sono i triangoli non degeneri aventi come vertici tre dei dieci punti dati?

22Considerate il numero 2002! = 1 × 2 × 3 × … × 2002. Chiaramente 2001 divide 2002! poiché 2002! = 2000! × 2001 × 2002. Il massimo valore k tale che 2001k divida 2002! è uguale a

23Due gruppi di amici formano una comitiva di più di 27 persone per gite in montagna. Alla prima gita hanno partecipato tutti tranne 12 persone del secondo gruppo, e in questa gita le persone del primo gruppo sono state più del doppio di quelle del secondo gruppo. Alla seconda gita hanno partecipato tutti tranne 10 persone del primo gruppo, e in questa gita le persone del secondo gruppo sono state più di 9 volte quelle del primo gruppo. Quante persone vi sono in ognuno dei due gruppi?

24Quanti triangoli non congruenti hanno come vertici tre dei vertici di un decagono regolare?

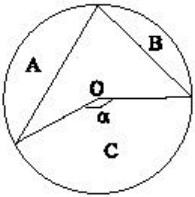
25La circonferenza della figura ha il centro nel punto O e il raggio unitario. La misura in radianti di ognuno degli angoli α, β e γ è minore di π. Se l'area della regione A vale 5π/12 - 1/4 e l'area della regione B vale π/4 - 1/2, allora l'area della regione C vale:

26Quanti numeri interi compresi tra 1 e 10²⁰⁰² hanno la somma delle cifre uguale a 2?

27Un aereo ideale vola da Milano nella direzione di Mosca. Esso parte con una velocità di 1 metro al secondo, ma raddoppia la sua velocità ad ogni metro percorso. Dopo quanto tempo dalla partenza sarà sulla verticale di Mosca (Mosca dista da Milano circa 2800 chilometri)?

28In un contenitore vi sono 21 litri di una soluzione con il 18% di alcool. Quanti litri di questo liquido si devono sostituire con una soluzione al 90% di alcool per ottenere una soluzione al 42% di alcool?

29a, b, c sono tre numeri tali che

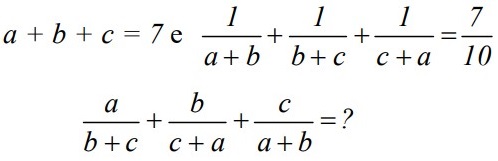
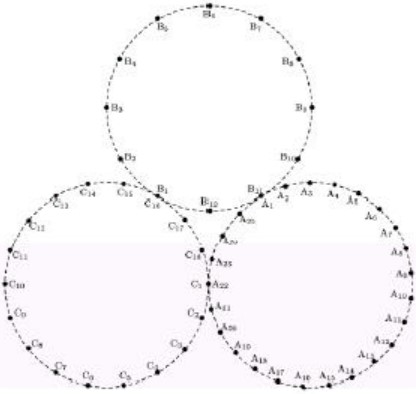
30L'immagine rappresenta un gioco da tavolo in cui le caselle sulle tre circonferenze sono state numerate da A1 a A25, da B1 a B12 e da C1 a C18. Una fiche è posta inizialmente nella casella A1 e può venire spostata in altre caselle secondo la regola seguente: ad ogni passo la fiche può essere spostata in una casella distante due posizioni, sulla stessa circonferenza, in qualsiasi direzione (per esempio una sequenza ammissibile è la seguente: C5 > C3 > C1 = A22 > A20 > A18 > A20); ma non è possibile muovere direttamente la fiche da C2 a A23. Quante sono le caselle inaccessibili per qualsiasi sequenza di mosse, partendo, come si è detto, dalla casella A1?