1Se si acquistano m penne al costo di n euro ciascuna e n penne al costo di m euro ciascuna, allora il costo medio in euro di ogni penna è:

2Una piramide ha 17 facce. Quanti sono i suoi spigoli?

3Il più piccolo numero reale x che verifica la disuguaglianza x² − 2004 < 0 è:

4Quanti sono i vertici di un poligono regolare la somma dei cui angoli interni è uguale a un settimo della somma degli angoli interni di un 16-gono regolare?

5s è un intero positivo dispari. In un quadrato di lato s i quadratini di lato 1 centrati sulle diagonali sono stati dipinti di nero (vedi l’esempio in figura, dove s = 7). Qual è l'area della regione non dipinta?

6Per definizione, in un gruppo di persone una “celebrità” è una persona del gruppo che è conosciuta da ogni altra persona del gruppo, ma che non conosce alcuna altra persona del gruppo. Consideriamo un gruppo di 100 persone: al suo interno il numero delle celebrità

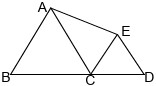
7I due triangoli equilateri ABC e ECD nella figura hanno lati di lunghezza 2 e 1 rispettivamente. L'area del quadrilatero ABCE è:

8Cinque persone scelgono un numero fra questi tre: 1, 2, 4. I cinque numeri scelti vengono moltiplicati fra loro. Uno solo fra i numeri seguenti potrebbe essere il prodotto ottenuto: quale?

9In un pascolo vi erano 15 pecore e alcuni pastori. Dopo che metà dei pastori e un terzo delle pecore si sono allontanati dal pascolo, vi è un totale di 50 gambe. Quante erano inizialmente le gambe?

10Un triangolo ABC è inscritto in una circonferenza il cui centro cade all’interno del triangolo e il cui raggio è lungo quanto il lato CB. Quanto misura in gradi l'angolo CÂB?

11Considera il piano cartesiano. Quanti sono i quadrati aventi un vertice in (-1,-1) e tali che almeno uno degli assi coordinati sia asse di simmetria del quadrato stesso?

12In una scatola non trasparente vi sono 100 carte, numerate da 1 a 100. Qual è il numero minimo di carte che dobbiamo estrarre al buio dalla scatola, per essere sicuri che il prodotto dei numeri che appaiono sulle carte estratte sia divisibile per quattro?

13Ogni marziano ha uno, due o tre tentacoli sulla propria testa. Esattamente l’1% della popolazione marziana consiste di individui con tre tentacoli, mentre il 97% consiste di individui con due tentacoli e il rimanente 2% ha un solo tentacolo. Quale percentuale di marziani ha più tentacoli sulla propria testa della media della totalità della popolazione marziana?

14Quanti sono i numeri di due cifre i cui quadrati e i cui cubi terminano con la stessa cifra?

15Quanti sono i numeri interi positivi che possono essere scritti nella forma a₀ + 3a₁ + 3²a₂ + 3³a₃ + 3⁴a₄ con a₀, a₁, a₂, a₃, a₄ appartenenti all'insieme {-1, 0, 1}?

16Il numero è

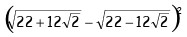
17Quanti sono i triangoli rettangoli i cui vertici sono tre tra i 14 vertici di un 14-gono regolare?

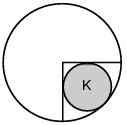
18Una circonferenza K è inscritta nel settore circolare che è un quarto di un cerchio di raggio 6, come mostrato in figura. Qual è il raggio di K?

19In una successione geometrica a₁, a₂, a₃, ... si hanno le seguenti disuguaglianze: a₃ < a₂ < a₄ . Allora sicuramente

20Qual è la penultima cifra di 11²⁰⁰⁴?

21In Ortolandia vi sono le elezioni. Ogni elettore del Partito dei Broccoli ha già mangiato broccoli, mentre il 90% degli elettori degli altri partiti non ha mai mangiato broccoli. Quale percentuale ha ottenuto il Partito dei Broccoli, se esattamente il 46% dei votanti ha già mangiato broccoli?

22Un parallelogramma è suddiviso in 4 triangoli, seguendo un criterio analogo a quello mostrato in figura. Allora :

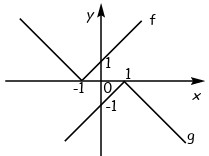
23La figura mostra i grafici di due funzioni f e g, definite sui numeri reali. Quale delle seguenti uguaglianze è soddisfatta, per ogni numero reale x ?

24Un triangolo equilatero ha lato 4. Il raggio dell'arco di circonferenza, centrata in uno qualunque dei vertici, che suddivide il triangolo in due parti aventi la stessa area, è:

25Partiamo con 200 numeri tutti uguali a zero scritti in successione. Al primo passaggio aggiungiamo 1 ad ognuno dei duecento numeri. Al secondo passaggio aggiungiamo 1 solo ai numeri il cui posto è un multiplo di 2 (cioè a quelli di posto pari). Al terzo passaggio aggiungiamo 1 solo ai numeri il cui posto è un multiplo di 3 e procediamo secondo questa legge: all'n-esimo passaggio aggiungiamo 1 solo ai numeri il cui posto è un multiplo di n. Dopo 200 passaggi, che numero troviamo al posto 120?

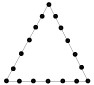
26Quanti sono i triangoli (non degeneri) i cui vertici sono 3 tra i 18 punti mostrati in figura?

27a, b, c sono tre cifre tali che 0 < a < b < c. La somma di tutti gli interi di tre cifre che possono essere formati permutando queste tre cifre è 1554. Che cifra è c ?

28Il numero n = 999 … 9 ha la rappresentazione decimale formata da 999 nove. Qual è la somma delle cifre di n² ?

29Quanti insiemi formati da numeri interi positivi consecutivi sono tali che la somma dei numeri che li costituiscono sia esattamente 100? (N.B. Si escluda l'insieme costituito dal solo numero 100).

30Sia ABCD un quadrilatero convesso di area unitaria, con AB e BD basi dei triangoli isosceli ABD e DBC rispettivamente. Sapendo inoltre che l’angolo BCD misura 100° e l’angolo ADB misura 20° (vedi figura), il prodotto AC x BD è uguale a: