120 x (0 + 6) - (20 x 0) + 6 =

2Lanciamo un dado (non truccato), con le facce numerate da 1 a 6. Quale dei seguenti eventi è il più probabile? L'uscita di un numero

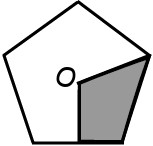
3Il punto O è il centro del pentagono regolare in figura. Quale percentuale del pentagono è ombreggiata?

4Una nonna dice ai nipoti: “Se preparassi 2 tortine per ognuno di voi, mi resterebbe pasta a sufficienza per fare esattamente altre 3 tortine. Non posso però fare 3 tortine per ciascuno di voi, poiché non avrei la pasta per le ultime 2 tortine.” Quanti nipoti ha quella nonna?

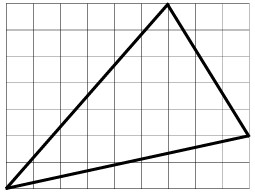
5La figura rappresenta un foglio quadrettato su cui è disegnato un triangolo. Se il lato di ogni quadretto misura 1 centimetro, l'area del triangolo vale (in centimetri quadrati)

6Una bottiglietta da 1/3 di litro è piena per 3/4. Quanti centilitri di liquido conterrà dopo averne versato in un bicchiere 20 centilitri?

7Un'indagine su 2006 studenti di Milano ha messo in luce che l'anno scorso 1500 di loro hanno partecipato alla gara matematica “Kangourou” e 1200 alla gara letteraria “Giovani scrittori”. Se solo 6 degli studenti intervistati non hanno partecipato ad alcuna gara, quanti hanno invece participato ad entrambe le gare?

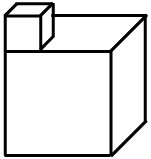
8Il solido in figura è formato da due cubi. Il più piccolo, il cui lato è lungo 1 centimetro, è interamente appoggiato sulla faccia superiore del cubo più grande il cui lato misura 3 centimetri. Quanto misura, in centimetri quadrati, la superficie totale del solido?

9Due lati di un triangolo (non degenere) misurano ciascuno 7 centimetri. La lunghezza del terzo lato è un numero intero di centimetri. Quanti centimetri può misurare al massimo il perimetro del triangolo?

10In una classe ci sono 21 studenti e in essa non ci sono due ragazze che siano amiche dello stesso numero di ragazzi della classe. Quante possono essere al massimo le ragazze in quella classe?

11Il mio astuccio è di un solo colore: se è blu, è tondo; se è quadrato, è rosso; è blu o giallo; se è giallo, è quadrato; è quadrato o tondo. Come è il mio astuccio?

12Andrea, Bruno e Carlo hanno unito i loro risparmi per acquistare una tenda da campeggio. Carlo ha contribuito per il 60% del prezzo, Andrea per il 40% della quota restante. Bruno ha aggiunto i 30 euro mancanti. Qual era il prezzo, in euro, della tenda?

13Due treni della stessa lunghezza stanno viaggiando uno incontro all'altro su una linea a doppio binario, il primo a 100 km/h e il secondo a 120 km/h. Quando si incrociano, da un finestrino del secondo treno un passeggero osserva che ci vogliono esattamente 6 secondi perché il primo treno gli sfili davanti completamente. In quanti secondi un passeggero del primo treno vede sfilare davanti a sè il secondo treno?

14Una comitiva di alieni attraversa lo spazio sull'astronave STAR 1. Sono di tre colori diversi: verde, lilla e blu. I verdi hanno due tentacoli, i lilla ne hanno tre e i blu ne hanno cinque. I verdi sono tanti quanti i lilla e i blu sono 10 più dei verdi. Insieme hanno 250 tentacoli. Quanti alieni blu viaggiano su STAR 1?

15Quando il canguro Jumpy si spinge con la gamba sinistra salta 2 metri; quando si spinge con la destra salta 4 metri; infine quando si spinge con entrambe le gambe, salta 7 metri. Qual è il minimo numero di salti sufficienti a Jumpy per coprire una distanza di 997 metri esatti?

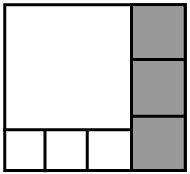
16Un rettangolo è diviso in 7 quadrati. Il lato dei quadrati grigi incolonnati a destra misura 8. Quanto misura il lato del grande quadrato bianco?

17Quale numero aumenta del 500% quando se ne fa il quadrato?

18Quanti triangoli isosceli (a due a due non congruenti) di area 1 hanno un lato lungo 2?

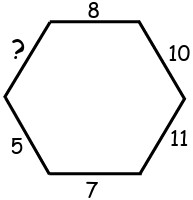
19In ciascuno dei vertici dell'esagono che vedi in figura c'era un certo numero di sassolini; su ciascun lato è riportata la somma dei sassolini che erano presenti nei due vertici adiacenti. Quanto vale la somma mancante?

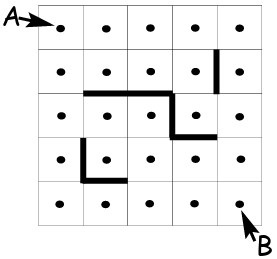
20In figura è rappresentato un quadrato suddiviso in 25 quadretti, in ciascuno dei quali è segnato il centro; con tratto più spesso sono segnati 3 ostacoli. Vogliamo andare da A a B passando da un centro all'altro solo per linee verticali e/o orizzontali, evitando gli ostacoli e per la via più breve. Quanti sono i cammini da A a B che rispettino tutte queste condizioni?

21Se il prodotto di due interi è uguale a 2⁵×3²×5×7³, allora la loro somma

22Se a e b sono due numeri interi positivi tali che a²b + ab² = 30 allora a + b + ab vale

23Sulla prima striscia vedi 11 carte, ciascuna con due lettere. Sulla seconda vedi le stesse carte ordinate in maniera diversa. Quale delle scritte che seguono può apparire nella seconda riga della seconda striscia di carte?

24Qual è la prima cifra del più piccolo numero intero positivo la somma delle cui cifre sia 2006?

25La mamma ha lavato le calze di Gianni - 5 paia nere, 10 paia marroni e 15 paia grigie - e gli ha chiesto di riporle dopo averle accoppiate per colore. Gianni invece le ha messe tutte mescolate in una scatola. Ora Gianni deve partire per un campeggio di 7 giorni: qual è il minimo numero di calze che gli basta estrarre dalla scatola, anche al buio, per essere sicuro di avere almeno 7 paia di calze ben accoppiate?

26Denota con E(n) la somma delle cifre dispari del numero n. Ad esempio E(7)=7, E(2)=0 ed E(3245)=8. Quanto vale E(1)+E(2)+E(3)+…+E(99)?

27Piero va in bicicletta da un punto P a un punto Q con velocità costante. Se aumentasse la sua velocità di 3 metri al secondo, arriverebbe a Q tre volte più in fretta (cioè impiegando un terzo del tempo). Quante volte più in fretta arriverebbe a Q, se aumentasse la sua velocità di 6 metri al secondo?

28Una locomotiva traina un treno di 5 vagoni, S, T, U, V e W. In quanti modi possono essere accostati i vagoni se la locomotiva deve risultare sempre più vicina al vagone S che al vagone T?

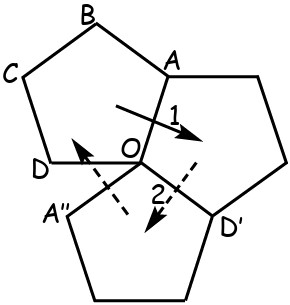
29In figura è rappresentato un pentagono regolare OABCD ed i pentagoni che da esso si ottengono facendo prima una rotazione di centro O che porti il lato OD a sovrapporsi al lato OA (e OA a OD'), poi una rotazione di centro O che porti il lato OA a sovrapporsi al lato OD' (e OD' a OA''). Continuando in questo modo, qual è il minimo numero di rotazioni sufficienti a riportare il pentagono nella posizione iniziale?

30Quanto vale a - b, se a = 1² + 2² + 3² + … + 2005² e b = 1x3 + 2x4 + 3x5 + … + 2004x2006?