14 × 4 + 4 + 4 + 4 + 4 + 4 × 4=?

2Due anni fa Anna aveva 8 volte l’età di suo fratello Billy. Oggi Anna ha 10 anni. Fra quanti anni Billy avrà 10 anni?

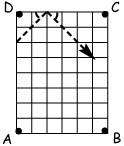
3Una palla di biliardo colpisce il bordo del tavolo con un angolo di 45°, come mostrato in figura. In quale delle buche cadrà?

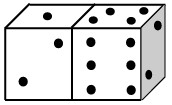
4Qual è la somma dei punti sulle facce dei due dadi che non sono visibili nella figura?

5Si vuol fare una coltura di ninfee in uno stagno. Ogni giorno la coltura raddoppia la sua estensione e se si mette a dimora una sola ninfea, dopo 12 giorni lo stagno è pieno. Dopo quanti giorni sarà pieno lo stagno se si mettono a dimora 4 ninfee?

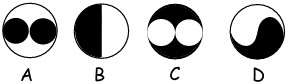
6In quale cerchio la parte nero è più estesa di quella bianca?

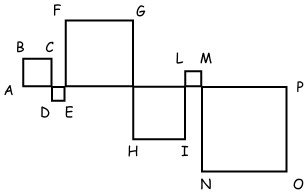
7I quadrati in figura sono stati formati intersecando il segmento AP lungo 24 centimetri con la linea spezzata ABC…OP. Quanti centimetri è lunga la spezzata ABC…OP?

8Un numero è detto palindromo se la sua rappresentazione decimale può essere indifferentemente letta da destra a sinistra o da sinistra a destra, come capita per esempio con 13931. Qual è la differenza tra il più grande numero palindromo di 6 cifre significative e il più piccolo di 5 cifre significative?

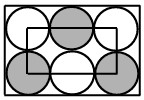
9Considera sei circonferenze dello stesso raggio disposte all’interno di un rettangolo grande, tangenti fra loro e tangenti i lati del rettangolo, come indicato in figura. I vertici del rettangolo piccolo sono situati ciascuno nel centro di una circonferenza. Il perimetro del rettangolo piccolo misura 60 centimetri. Quanti centimetri misura il perimetro di quello grande?

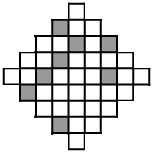
10Vogliamo fare in modo che la figura a fianco presenti un asse di simmetria. Qual è il più piccolo numero di quadratini che basta annerire per ottenere lo scopo?

11Qual è il più piccolo numero primo che divide la somma 3¹¹ + 5¹³ ?

12In una classe mista il numero delle ragazze è inferiore di tre a quello dei ragazzi. Ogni ragazzo è amico esattamente di quattro ragazze, mentre ogni ragazza è amica esattamente di cinque ragazzi (naturalmente l’amicizia è reciproca). Quante persone vi sono in quella classe?

13Sei diversi punti sono individuati su due rette parallele: quattro su una e due sull’altra. Quanti sono i triangoli che hanno per vertici i punti in questione?

14Un sondaggio ha rivelato che, tra i consumatori di cioccolata del paese di Dolcezza, 2/3 comprano la marca A e 1/3 la marca B. Un nuovo sondaggio, svolto dopo una campagna pubblicitaria in favore della marca B, ha evidenziato che 1/4 dei consumatori che prima preferivano A ora sono passati a B. La frazione di consumatori che adesso comprano A è

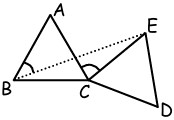
15I triangoli ABC e CDE in figura sono congruenti e equilateri. Se l’angolo ACE misura 80 gradi, quanti gradi misura l’angolo ABE?

16Considera tutti i numeri interi da 1 a 10000. Quale percentuale di essi è un quadrato perfetto?

179 rette, di cui 5 tracciate orizzontalmente e 4 verticalmente, individuano 12 celle rettangolari; invece 6 rette orizzontali e 3 verticali individuano solo 10 celle. Quante celle puoi ottenere al massimo tracciando 15 rette?

18Hai un foglio di carta rettangolare con un lato doppio dell’altro. Ci sono due cilindri che possono essere “fasciati” esattamente dal foglio, congiungendo senza sovrapposizioni lati opposti del foglio. Chiama C₁ il cilindro fasciato dal foglio quando accosti i lati corti e C₂ quello fasciato dal foglio quando accosti i lati lunghi e denota rispettivamente con V₁ e V₂ i loro volumi. Quale delle seguenti affermazioni è corretta?

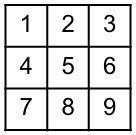
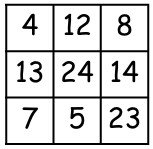
19Togliamo tre numeri dalla griglia qui a lato, in modo che dopo averli tolti nessuna riga e nessuna colonna rimanga completa; sommiamo quindi i numeri tolti. Qual è la somma più grande che si riesce ad ottenere?

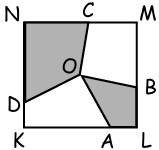
20Nella figura a fianco O è il centro del quadrato KLMN e i punti su ciascun lato di KLMN sono scelti con l’unico vincolo che il segmento OA sia perpendicolare al segmento OD e il segmento OB sia perpendicolare al segmento OC. Se il lato del quadrato misura 2, quanto misura l’area della regione ombreggiata?

21Una calcolatrice mal funzionante non mostra mai la cifra 1. Ad esempio se si digita 3131 compare solo il numero 33, senza spazi. Marco ha digitato un numero di 6 cifre, ma è comparso solo il numero 2007: quanti numeri devo elencare per essere certo di dire il numero digitato da Marco?

22Alfredo esce per una passeggiata: il primo tratto di strada è pianeggiante, il secondo in salita. Ritorna per la stessa strada e complessivamente impiega due ore. La sua velocità è di 4 km/h sul terreno pianeggiante, di 3 km/h in salita e di 6 km/h in discesa. Per quanti chilometri ha camminato Alfredo?

23Anna e Bice insieme pesano meno di quanto pesano insieme Carla e Dina; Carla ed Emma insieme pesano meno di quanto pesano insieme Franca e Bice. Quale delle seguenti affermazioni è certamente vera?

24La prima cifra di un numero di quattro cifre è uguale al numero di cifre 0 di quel numero, la seconda cifra è uguale al numero di cifre 1, la terza è uguale al numero di cifre 2, la quarta è uguale al numero di cifre 3. Quanti sono i numeri con questa proprietà?

25Comprendendo tra i divisori di un numero il numero stesso e l’unità, un intero positivo n ha due divisori mentre n + 1 ne ha tre. Quanti sono i divisori di n + 2?

26Su un tavolo sono disposte 9 carte su ciascuna delle quali appare un numero, come in figura. Gigi e Piero rimuovono ciascuno quattro carte: la somma dei numeri scritti sulle carte rimosse da Gigi è tre volte quella dei numeri scritti sulle carte rimosse da Piero. Quale numero è scritto sulla carta che rimane in tavola?

27Cinque numeri interi sono scritti su una circonferenza in modo che nessuna coppia e nessuna terna di numeri adiacenti dia una somma divisibile per 3. Tra questi numeri quanti sono divisibili per 3?

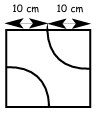
28In figura è mostrata una piastrella quadrata di lato 20 cm, con due motivi decorativi a forma di quarto di circonferenza di raggio 10 cm, centrate in vertici opposti del quadrato. Pavimentiamo con piastrelle come questa una superficie quadrata di lato 80 cm in modo che gli archi si connettano a due a due. Qual è la lunghezza in centimetri della più lunga curva connessa che può venire a formarsi in questo modo?

29Un numero intero di tre cifre è stato diviso per 9: la somma delle cifre del quoziente è inferiore di 9 alla somma delle cifre del numero di partenza. Quanti numeri di tre cifre hanno questa proprietà?

30Uno strano calcolatore può fare solo le seguenti operazioni: moltiplicare per 2 o per 3, oppure elevare alla potenza 2 o alla potenza 3. Partendo dal numero 15, quale dei seguenti numeri può essere ottenuto con 5 operazioni successive di questo calcolatore?