1Quanti quadrati si possono tracciare che abbiano come vertici quattro dei punti in figura?

2Una classe è composta da 9 ragazzi e 13 ragazze. Metà di loro ha l’influenza. Qual è il minimo numero di ragazze che hanno sicuramente l’influenza?

3In una gara sono assegnati 12 quesiti: gli elaborati sono stati distribuiti tra i membri della commissione giudicatrice in modo che tutti gli elaborati relativi ad un quesito siano valutati da due commissari e che ogni commissario valuti gli elaborati di tre quesiti. Quanti sono i membri della commissione?

4I numeri 2, 3, 4, insieme ad un altro numero sconosciuto, sono scritti nella griglia 2×2 a lato, uno per ogni casella. Si sa che la somma dei numeri della prima riga vale 9 e che la somma dei numeri della seconda riga vale 6. Il numero sconosciuto è

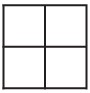
5Pierino crede che, se un triangolo è isoscele, allora tutti i suoi angoli siano acuti. Quale delle seguenti figure può convincerlo del contrario?

6Una fioraia ha a disposizione 24 rose bianche, 42 rosse e 36 gialle. Vuole comporre tanti mazzi identici, utilizzando tutti i fiori. Quanti mazzi può comporre al massimo?

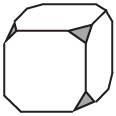
7Ad un cubo sono stati segati tutti suoi vertici, come è illustrato dalla figura. Quanti spigoli possiede il nuovo solido così ottenuto?

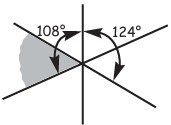
8In figura sono rappresentate tre rette a, b, c che si intersecano in un punto, formando angoli l’ampiezza di due dei quali (in gradi) è indicata in figura. Quanti gradi misura l’angolo dipinto di grigio?

9Daniele ha 9 monete, ciascuna da 2 centesimi; sua sorella Anna ha 8 monete, ciascuna da 5 centesimi. Qual è il minimo numero di monete che devono cambiare proprietario perché ciascuno abbia la stessa quantità di denaro?

10Alcuni amici si salutano: ciascuno stringe la mano a tutti gli altri. Se le strette di mano sono state 15, quanti sono gli amici?

11I due autobus che prestano servizio sulla linea circolare intorno a Kangcity passano da una certa fermata a intervalli regolari di 25 minuti. Quanti autobus bisogna aggiungere sulla linea per accorciare l’intervallo di attesa del 60%?

12Il matematico francese August de Morgan, morto nel 1899, soleva dire di aver avuto x anni nell’anno x². Quando nacque de Morgan?

13Vogliamo visitare quattro isole A, B, C, D partendo dalla terraferma, utilizzando i traghetti che le collegano. C è collegata nei due versi con la terraferma; A e C sono collegate tra loro nei due versi come pure A e D. A e B possono essere solo raggiunte dalla terraferma come A da B. Qual è il minimo numero di corse sufficiente a visitare tutte le isole (con partenza e arrivo sulla terraferma)?

14Tom e Jerry hanno ciascuno un rettangolo. I due rettangoli sono uguali. Ciascuno taglia il proprio. Tom ottiene due rettangoli ognuno dei quali ha perimetro di 40 cm, mentre Jerry ottiene due rettangoli ognuno dei quali ha perimetro di 50 cm. Qual era il perimetro di ciascuno dei rettangoli iniziali?

15Una faccia di un cubo è tagliata lungo le sue due diagonali. Quali dei seguenti non sono sviluppi piani di tale cubo?

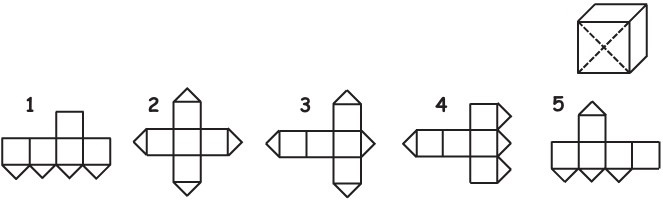
16Su questa griglia sono evidenziati 5 punti. Fra tutte le spezzate congiungenti i 5 punti formate da 4 segmenti consecutivi, quante sono quelle che suddividono il quadrato in due regioni di uguale area?

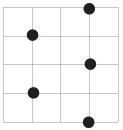
17Quattro cerchi congruenti di raggio 6 centimetri sono tangenti tra loro e ai lati del rettangolo come in figura. Se P è un vertice del rettangolo e Q ed R sono punti di tangenza, quanti centimetri quadrati misura l’area del triangolo PQR?

18Una scatola contiene sette carte numerate da 1 a 7. Due saggi pescano a caso delle carte dalla scatola: il primo ne prende tre, il secondo due delle rimanenti; le ultime due restano chiuse nella scatola. Il primo saggio, dopo aver guardato solo i numeri scritti sulle carte da lui pescate, dice al secondo: “Sono certo che la somma dei numeri riportati sulle tue carte è pari”. Quanto vale la somma dei numeri riportati sulle carte pescate dal primo saggio?

19Lucia e Carlo partono per un’escursione in montagna. Alla partenza leggono su un segnavia che la loro destinazione si trova a 2 ore e 55 minuti di cammino. Lasciano il villaggio alle 12 in punto e alle 13 esatte fanno la prima sosta e leggono su un altro segnavia che la loro destinazione è solo a 1 ora e 15 minuti di distanza. Dopo un quarto d’ora di sosta continuano l’escursione alla stessa velocità di prima e senza soste. A che ora arrivano a destinazione?

20Su una retta sono segnati dei punti. Alcune delle distanze tra di essi sono: 1 cm, 2 cm, 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, 9 cm. Qual è il minimo numero di punti che permette di realizzare questa condizione?

21Nell’uguaglianza KAN – GAR = OO ogni lettera rappresenta una cifra (in notazione decimale): lettere diverse rappresentano cifre diverse, lettere uguali rappresentano cifre uguali. Qual è il massimo valore che può essere assunto dal numero KAN?

22In una compagnia le ragazze sono più del 45% ma meno del 50%. Qual è il minimo numero di ragazze che devi pensare facciano parte di tale compagnia?

23Un ragazzo dice sempre il vero al giovedì e al venerdì, mente sempre al martedì, mentre negli altri giorni della settimana mente o dice la verità senza una regola. Gli è stato chiesto il suo nome per sette giorni di fila e nei primi sei ha fornito nell’ordine le seguenti risposte: Luca, Mario, Luca, Mario, Piero, Mario. Che cosa ha risposto il settimo giorno?

24Matilde ha disegnato 36 canguri usando tre colori distinti. Il bianco è stato usato per 25 canguri, il rosso per 28 e il nero per 20. Solo per 5 canguri sono stati usati tutti e tre i colori. Quanti dei canguri disegnati sono di un solo colore?

25Chiamiamo “speciale” una terna di numeri primi positivi se il loro prodotto è uguale a cinque volte la loro somma. Quante terne speciali esistono?

26Siano A l’insieme dei numeri di 5 cifre tali che il prodotto delle loro cifre è 25 e B l’insieme dei numeri di 5 cifre tali che il prodotto delle loro cifre è 15. Quale dei due insiemi contiene più elementi? Qual è il rapporto tra il numero di elementi dell’insieme più numeroso e il numero di elementi dell’altro?

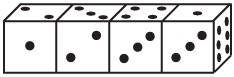
27Quattro dadi identici sono accostati come in figura. Le facce di ciascun dado sono numerate da 1 a 6, ma i dadi non sono standard, cioè la somma dei punti di due facce opposte può non valere 7. Qual è la somma totale dei punti che compaiono sulle 6 facce ciascuna delle quali viene a contatto con qualche altra faccia?

28Per ogni numero di due cifre, sottraiamo la cifra delle unità da quella delle decine. Quanto vale la somma di tutte queste differenze?

29Il massimo comun divisore di due numeri interi positivi m e n è 12 e il loro minimo comune multiplo è un quadrato perfetto. Allora quanti dei 5 numeri razionali n/3, m/3, n/4, m/4, m×n sono dei quadrati perfetti?

30Denotiamo con M il prodotto del perimetro di un triangolo per la somma delle tre altezze dello stesso triangolo. Quale delle seguenti affermazioni è falsa se l'area del triangolo vale 1?