1In una stanza ci sono cani e gatti. Il numero delle zampe di gatto è il doppio del numero dei nasi di cane. Allora il numero dei gatti è

2Ad una festa da ballo hanno partecipato 4 ragazze e 4 ragazzi. Alla fine i quattro ragazzi dichiarano di aver ballato con 3, 1, 2, 2 diverse compagne mentre tre delle ragazze dichiarano di aver ballato ciascuna con 2 diversi compagni. Con quanti compagni diversi ha ballato la quarta ragazza?

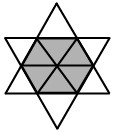
3La stella rappresentata in figura è formata da 12 triangoli equilateri identici. Il perimetro della stella è di 36 cm. Quanti centimetri misura il perimetro dell’esagono ombreggiato?

4Le case presenti in via Lunga sono numerate a partire da 1, senza saltare numeri. Enrico deve consegnare delle lettere in alcune case: precisamente deve consegnare una lettera in ciascuna casa che abbia un numero civico dispari, iniziando dalla casa numero 15 e finendo con la casa numero 53. Quante lettere deve consegnare in tutto?

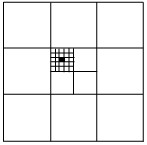
5In figura è rappresentato un quadrato suddiviso in quadrati via via più piccoli. Se il quadrato più grande ha area 1, quanto vale l’area del quadratino nero?

6Il prodotto di quattro diversi interi positivi è 100. Qual è la loro somma?

7Un ascensore può trasportare fino a 12 adulti oppure fino a 20 bambini. Quanti bambini possono salire al massimo insieme a 9 adulti?

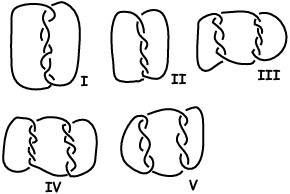
8La figura mostra cinque intrecci di corde. Quali di essi non possono essere realizzati con un unico spezzone di corda?

9Un recipiente a forma di parallelepipedo rettangolo ha dimensioni tali che, riempito fino all’orlo, contiene un litro d’acqua. Ognuna delle sue tre dimensioni viene dimezzata, creando un nuovo recipiente della stessa forma. Se anche questo recipiente viene riempito fino all’orlo, quanti litri d’acqua contiene?

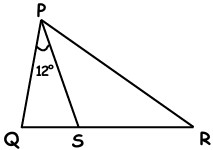
10I punti Q, R e S rappresentati in figura sono allineati, l’angolo QPS misura 12 gradi e i segmenti PQ, PS e RS hanno la stessa lunghezza. Quanti gradi misura l’angolo QPR?

11Quanti numeri interi positivi N hanno la seguente proprietà: “il numero di cifre della rappresentazione decimale del quadrato di N è uguale al numero di cifre della rappresentazione decimale del cubo di N”?

12Qual è il più piccolo numero di punti che basta rimuovere dalla figura perché tra i punti che restano non ce ne siano tre allineati?

13Nicola ha misurato i sei angoli di due triangoli, uno acutangolo, l’altro ottusangolo. Ricorda le misure di quattro di questi angoli: 120°, 80°, 55° e 10°. Quanti gradi misura l’angolo più piccolo nel triangolo acutangolo?

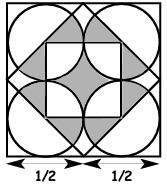
14Il quadrato più grande rappresentato in figura ha area 1. Qual è l’area della regione ombreggiata?

15Su un’isola vivono due categorie di persone: i sinceri, che non mentono mai, e i bugiardi, che mentono sempre. Su quest’isola ci sono 25 persone in fila. Ognuno, tranne il primo della fila, dice che la persona davanti a lui nella fila è un bugiardo mentre il primo dice che tutti quelli dietro di lui sono bugiardi. Quanti bugiardi ci sono nella fila?

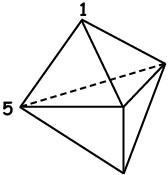
16Il solido in figura ha 6 facce, tutte triangolari. Ad ogni suo vertice viene associato un numero in modo che la somma dei numeri associati ai tre vertici di ogni singola faccia sia la stessa per tutte le facce. La figura indica i numeri associati a due dei vertici. Quanto vale la somma di tutti i numeri impiegati?

17Nell’uguaglianza lettere diverse rappresentano cifre diverse, mentre lettere uguali rappresentano cifre uguali. Quanti valori differenti può assumere il prodotto O•T•T•O?

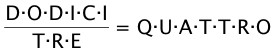
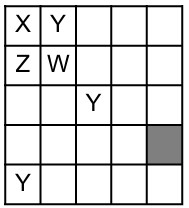
18Vogliamo colorare le celle della griglia in figura usando i quattro colori diversi X, Y, Z, W in modo che due celle che sono a contatto non ricevano mai lo stesso colore (due celle si considerano a contatto se hanno in comune almeno un vertice). La figura mostra che alcuni colori sono già stati assegnati. Con quali colori può essere colorata la cella ombreggiata?

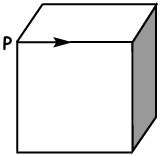
19In figura è rappresentato un poligono regolare con 9 lati. Quanti gradi misura l’angolo X evidenziato in figura, realizzato prolungando due dei lati?

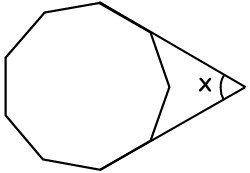
20In figura sono mostrati i primi tre disegni di una sequenza: ciascuno di essi è costituito da quadratini di lato 1 che circondano nel modo indicato un buco quadrato (grigio in figura). Quanti quadratini di lato 1 sono necessari per costruire il decimo disegno della sequenza?

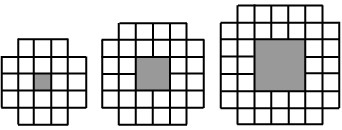
21Ci muoviamo lungo gli spigoli del cubo in figura partendo dal punto P, nella direzione indicata dalla freccia. Alla fine del primo spigolo dobbiamo decidere se andare a destra o a sinistra e così pure alla fine di ogni spigolo che percorriamo successivamente: scegliamo alternando destra e sinistra. Quanti spigoli avremo percorso quando torneremo per la prima volta nel punto P?

22Quanti sono i numeri interi positivi di dieci cifre contenenti solo le cifre 1, 2 e 3 nei quali due qualsiasi cifre adiacenti differiscono di 1?

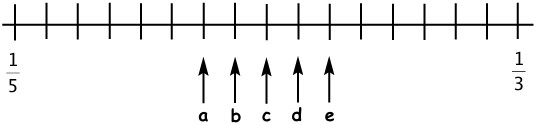
23In figura è rappresentato il segmento di retta numerica compreso tra le frazioni 1/5 e 1/3, suddiviso da tacche in segmenti di ugual lunghezza. Allora 1/4 corrisponde alla tacca indicata con

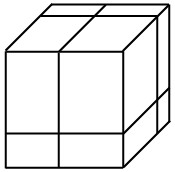
24Con tre tagli abbiamo suddiviso un grande cubo in otto parallelepipedi rettangoli. Qual è il rapporto tra la somma delle superfici totali di questi otto parallelepipedi e la superficie totale del cubo originario?

25Quanti numeri interi positivi N soddisfano la seguente condizione: tra tutti i divisori di N, diversi da N e da 1, il maggiore è 45 volte il minore?

26Un quadrato è stato suddiviso esattamente (cioè senza avanzi e senza sovrapposizioni) in 2009 quadrati. Se la lunghezza del lato di ciascuno dei quadrati di cui si parla è un numero intero, qual è la minima lunghezza del lato del quadrato originario che rende possibile questa scomposizione?

27In un quadrilatero non intrecciato PQRS il lato PQ misura 2006, il lato QR misura 2008, il lato RS misura 2007 e il lato SP misura 2009. Quali angoli interni del quadrilatero sono necessariamente minori di 180°?

28Sovrapponendo un quadrato di lato 6 centimetri a un triangolo posso coprire al massimo il 60% della superficie di tale triangolo. Sovrapponendo il triangolo al quadrato posso coprire al massimo i 2/3 della superficie del quadrato. Qual è in centimetri quadrati l’area del triangolo?

29Pinocchio ha scritto in sequenza alcuni numeri interi positivi tutti diversi fra loro e minori di 11. Il Grillo parlante osserva che in ogni coppia di numeri adiacenti, così come li ha allineati Pinocchio, ce n’è uno che è divisibile per l’altro. Quanti numeri può aver scritto al massimo Pinocchio?

30In un triangolo ABC l’angolo in B misura 20 gradi e l’angolo in C misura 40 gradi. La lunghezza della bisettrice dell’angolo in A è 2. Quanto vale la differenza fra la lunghezza di BC e la lunghezza di AB?