1Quanto vale 12 + 23 + 34 + 45 + 56 + 67 + 78 + 89?

2Quanti assi di simmetria si possono individuare nella figura contenuta nel quadrato?

3Alcuni canguri giocattolo sono confezionati singolarmente in scatole a forma di cubo e tutte le scatole sono uguali fra loro. Esattamente 64 di queste scatole sono impacchettate strettamente in una scatola di cartone, anch’essa a forma di cubo. Quanti canguri alloggiano al piano inferiore di tale scatola?

4La nonna ha fatto una torta per i nipotini che verranno a trovarla nel pomeriggio, ma non si ricorda più se ne verranno 3, 5 o 6. Intende tagliarla in parti uguali prima del loro arrivo ed essere sicura che ciascun nipote riceva la stessa quantità di torta. Per essere preparata a ciascuna delle tre eventualità, in quante fette è opportuno che tagli la torta?

5I punti disegnati in figura sono i vertici di un esagono regolare. Congiungendone alcuni con segmenti, puoi ottenere diverse figure geometriche, ma sicuramente non puoi ottenere

6Ho scritto sette numeri interi consecutivi. Se la somma dei tre più piccoli è 33, quanto vale la somma dei tre più grandi?

7Da un certo numero di tronchi un taglialegna ha ricavato 72 ceppi di legna da ardere. Pur segando un tronco alla volta, gli sono bastati 53 tagli. Quanti erano i tronchi all’inizio?

8Nella scatola, che in figura vedi dall’alto, ci sono sette barrette uguali: ognuna di esse ha base rettangolare di lati 1 cm e 3 cm. È possibile far scivolare alcune barrette senza sollevarle in modo che nella scatola ci sia posto per un’altra barretta con le stesse misure? In caso di risposta affermativa, qual è il minimo numero di barrette che basta far scivolare?

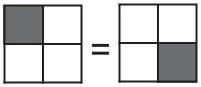
9Un quadrato è suddiviso in quattro quadratini di uguale misura. Ognuno di questi quadratini deve essere colorato di bianco o di grigio. Quante sono le diverse colorazioni possibili per il quadrato? (Due colorazioni sono considerate diverse se non si possano ottenere una dall’altra ruotando il quadrato)

10Sottraendo la somma dei primi 100 numeri (interi) dispari positivi dalla somma dei primi 100 numeri (interi) pari positivi si ottiene

11Tre martedì di un certo mese sono giorni con data pari. In che giorno della settimana cade il 21 di quel mese?

12Qual è il più piccolo numero di due cifre che non è esprimibile come somma di tre diversi numeri di una cifra?

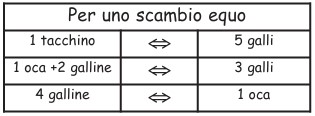
13Al mercato del baratto le merci vengono scambiate secondo la lista dei prezzi riportata a fianco. Renzo vuole portare a casa un’oca, un tacchino ed un gallo. Qual è il minimo numero di galline che gli basta portare al mercato?

14Nel quadrilatero ABCD i lati AD e BC sono uguali e, come indicato in figura, l’angolo DAC misura 50 gradi, l’angolo DCA misura 65 gradi, l’angolo ACB misura 70 gradi. È possibile stabilire con certezza quanti gradi misura l’angolo ABC?

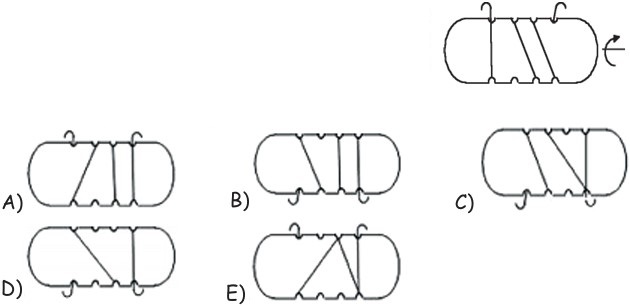
15Chiara ha avvolto del filo intorno ad un cartone sagomato, come suggerito dalla figura. Poi ha ruotato il cartone di 180 gradi intorno al suo asse, come indicato in figura. Quale delle seguenti immagini vede dopo la rotazione?

16In una scatola ci sono 50 mattoncini, ciascuno di un solo colore: bianco, giallo o rosso. Il numero di quelli bianchi è undici volte il numero di quelli gialli e ci sono meno mattoncini rossi che bianchi, ma più rossi che gialli. Allora il numero di mattoncini rossi è inferiore al numero di mattoncini bianchi di

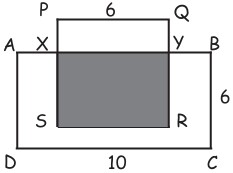
17A lato sono raffigurati un rettangolo ABCD e un quadrato PQRS, insieme alle misure dei loro lati. La regione ombreggiata ha area metà dell’area del rettangolo ABCD. Qual è la lunghezza del segmento PX?

18Qual è il più piccolo numero di rette che basta tracciare per suddividere il piano in esattamente 5 regioni?

19Le lettere a, b, c, d, e rappresentano dei numeri tali che a – 1 = b + 2 = c – 3 = d + 4 = e – 5. Quale lettera rappresenta il numero più grande?

20In figura è riprodotto un logo disegnato accostando archi semicircolari i cui raggi misurano 2 cm, 4 cm o 8 cm. Quale frazione del logo è ombreggiata?

21Le circonferenze rappresentate in figura delimitano al loro interno complessivamente nove regioni. In ciascuna regione si scrive uno e un solo numero da 1 a 9 in modo che tutti i numeri compaiano e che la somma dei numeri in ciascun cerchio sia esattamente 11. Quale numero deve essere scritto nella regione indicata dal punto interrogativo?

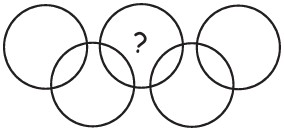
22In un supermercato vi sono due file di carrelli tutti uguali fra loro formate nel modo usuale, cioè infilando un carrello in quello che lo precede. Una fila è formata da 10 carrelli ed è lunga 2.9 metri, l’altra da 20 carrelli ed è lunga 4.9 metri. Quanto è lungo un carrello?

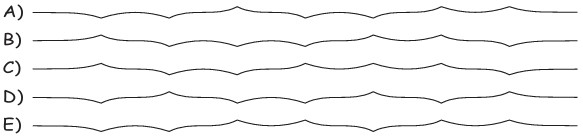
23Una lunga striscia di carta è stata piegata a metà tre volte, ogni volta senza riaprire la piegatura precedente; poi è stata riaperta e appoggiata su un tavolo: guardandola di profilo, si vedono ancora le 7 pieghe e i tratti della striscia tra essi compresi. L’aspetto della striscia di profilo può assomigliare solo a quattro delle linee disegnate sotto: quale è quella da scartare?

24Hai 18 cartoncini su ciascuno dei quali sta scritto uno solo numero: 4 oppure 5. La somma di tutti i numeri sui cartoncini è divisibile per 17. Su quanti cartoncini è scritto il numero 4?

25Ogni numero naturale da 1 a 10 è stato scritto una e una sola volta su una lavagna. Uno studente cancella due numeri dalla lavagna e al loro posto scrive la loro somma diminuita di uno; poi un altro studente cancella due dei numeri sulla lavagna e scrive al loro posto la loro somma diminuita di uno e così via finché sulla lavagna resta un solo numero. Il numero rimasto

26In una città vivono solo gentiluomini e bugiardi. Ogni singola affermazione pronunciata da un gentiluomo è vera, mentre ogni singola affermazione pronunciata da un bugiardo è falsa. Alcuni abitanti sono riuniti in una stanza e tre di loro fanno, una per ciascuno, le seguenti coppie di affermazioni: 1.“Non ci sono più di tre persone in questa stanza.” “Tutti noi mentiamo.” 2.“Non ci sono più di quattro persone in questa stanza.” “Non siamo tutti bugiardi.” 3.“Ci sono cinque persone in questa stanza.” “Tre di noi sono bugiardi.” Quante persone ci sono nella stanza e quanti bugiardi ci sono tra di loro?

27Andrea ha un sacco pieno di cubetti. Ognuno di essi ha lato 1 ed è colorato di un solo colore. Andrea vuole usare 27 cubetti per formare un cubo di lato 3 tale che, se due cubetti hanno almeno un vertice in comune, i loro colori siano diversi. Qual è il minimo numero di colori che gli basterà usare?

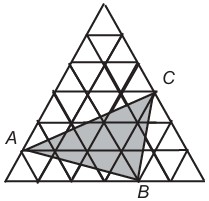
28In figura vedi un triangolo equilatero grande costruito accostando 36 triangolini, pure equilateri, ciascuno di area 1 cm2. Quanti centimetri quadrati misura l’area del triangolo ABC?

29x e y denotano due numeri interi positivi. Il minimo comune multiplo tra 24 e x è minore del minimo comune multiplo tra 24 e y. Allora y/x non può essere uguale a

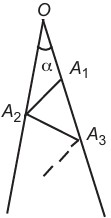
30L’angolo α rappresentato in figura misura 7 gradi; i punti A₁, A₃, … (indice dispari) sono presi in sequenza su un lato dell’angolo, mentre i punti A₂, A₄, … (indice pari) sono presi in sequenza sull’altro lato in modo che i segmenti OA₁, A₁A₂, A₂A₃, … siano tutti distinti, ma di uguale lunghezza. Una volta fissata tale lunghezza, il valore di n per cui il punto An ha la massima distanza possibile da O