1Lancia un dado tradizionale: qual è la probabilità che il prodotto dei numeri che compaiono sulle cinque facce che rimangono visibili sia divisibile per 6?

2In una lotteria vengono premiati tutti e soli i possessori di biglietti il cui numero sia composto da almeno cinque cifre, delle quali al più tre siano maggiori di 2. Tra i possessori dei seguenti biglietti 1022, 22222, 102334, 213343, 3042531 quanti vengono premiati?

3Un pallone aerostatico è fermo a 1200 metri di altezza sul suolo. Il personale a bordo possiede una rice-trasmittente in grado di operare nel raggio di 1300 metri. Qual è la massima distanza in metri di due persone a terra che, munite di analoghe rice-trasmittenti, possono comunicare con il personale a bordo?

4Sia ABC un triangolo di area 96. Siano D il punto medio del lato AB, E il punto medio del segmento DB, F il punto medio del lato BC. Quanto vale l’area del triangolo AEF ?

5Un organismo internazionale è attualmente composto da 32 membri. Da quanti membri sarà composto fra tre anni, se ogni anno il numero dei membri è superiore del 50% rispetto all’anno precedente?

6Osserva la griglia in figura. Una mossa consiste esclusivamente nello spostare (in orizzontale, in verticale o in diagonale) una pedina da una casella ad un’altra adiacente. Vuoi spostare una pedina da una delle due caselle marcate con il triangolo sull’altra, impiegando il minor numero possibile di mosse. Quanti percorsi diversi hai a disposizione?

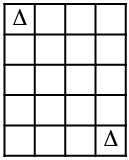
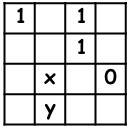
7In ogni cella della griglia in figura va inserita la cifra 0 oppure la cifra 1, facendo in modo che in ogni riga e in ogni colonna la somma delle cifre che vi compaiono sia 2. Quali cifre occorre sostituire a X e a Y?

8Trova il massimo valore che può assumere l’espressione KAN + GA + ROO quando ad ogni lettera viene fatta corrispondere una cifra, in modo che a lettere diverse corrispondano cifre diverse.

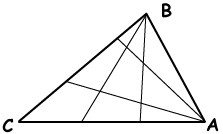
9Nella figura vedi un triangolo ABC in cui dal vertice A partono due diversi segmenti con secondo estremo sul lato opposto, e lo stesso accade dal vertice B. I quattro segmenti così tracciati ripartiscono il triangolo in 9 regioni disgiunte (salvo per i bordi). Se da ciascuno dei due vertici A e B si tracciano quattro diversi segmenti, invece di due, fino ad incontrare il lato opposto, qual è il numero di regioni (disgiunte, salvo per i bordi) in cui risulta ripartito il triangolo?

10Qual è il massimo numero di mesi di uno stesso anno che possono avere cinque domeniche?

11Gli abitanti di un’isola si dividono in mentitori (persone che mentono sempre) o sinceri (persone che dicono sempre la verità). Un giorno 12 abitanti, fra cui vi sono sia sinceri sia mentitori, si trovano insieme e fanno alcune dichiarazioni. Due di essi dicono: “Esattamente due di noi 12 sono mentitori”. Altri quattro dicono: “Esattamente quattro di noi 12 sono mentitori”. I restanti sei dicono: “Esattamente sei di noi 12 sono mentitori”. Quanti mentitori vi sono fra quei 12?

12A quale potenza dobbiamo elevare 4⁴ per ottenere 8⁸ ?

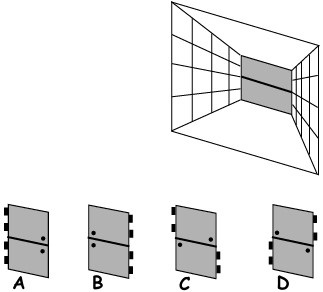
13Delle quattro pareti che delimitano un cunicolo, le due laterali (opposte) sono verticali mentre pavimento e soffitto sono paralleli fra loro, ma non perpendicolari alle pareti laterali: di conseguenza la sezione verticale non è un rettangolo, ma un parallelogramma che, osservato dall’ingresso, presenta la parte più bassa sulla destra. A metà del cunicolo si vuole costruire una porta di sbarramento che sia costituita da due sezioni, superiore e inferiore, apribili l’una indipendentemente dall’altra. Guardando dall’ingresso, come vanno incernierate le due sezioni?

14Una classe ha affrontato uno dei problemi di Kangourou. Il numero dei ragazzi che hanno risolto il problema coincide con il numero delle ragazze che non l’hanno risolto. È maggiore il numero di coloro (ragazzi e ragazze) che hanno risolto il problema o il numero complessivo delle ragazze?

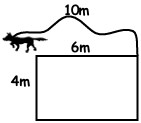
15Osserva la figura. Uno dei due estremi di una corda lunga 10 metri è fissato ad un angolo di un capanno a pianta rettangolare di 4 metri per 6 metri, mentre all’altro estremo è legato un cane (che non può ovviamente entrare nel capanno). Qual è il perimetro della regione entro la quale può muoversi il cane?

16Sono le 21:00 e sto guidando alla velocità di 100 km/h. A questa velocità con la benzina che mi resta posso percorrere solo 80 km, ma il distributore più vicino è distante 100 km. La quantità di benzina che la mia auto consuma è direttamente proporzionale alla velocità dell’auto e io desidero perdere quanto meno tempo è possibile. A che ora arriverò al distributore?

17Un trapezio è costruito a partire da un triangolo equilatero “segandone un angolo” (cioè sopprimendo da esso un opportuno triangolo più piccolo avente un vertice in comune con esso). Due copie di questo trapezio vengono accostate in modo da formare un parallelogramma il cui perimetro risulta 10 centimetri più lungo del perimetro del triangolo originale. Quanti centimetri misura il perimetro del triangolo originale?

18L’orologio della nonna ogni giorno, rispetto alla marcia corretta, 1)tra le 0:00 e le 6:00 va avanti di 15 secondi; 2)tra le 6:00 e le 12:00 resta indietro di 10 secondi; 3)tra le 12:00 e le 18:00 va avanti di 15 secondi; 4)tra le 18:00 e le 24:00 resta indietro di 10 secondi. Oggi, 15 marzo, a mezzogiorno l’orologio segna l’ora esatta. Se la nonna non regolerà più l’orologio, a che ora di quale giorno il suo orologio segnerà per la prima volta esattamente 5 minuti in più rispetto all’ora esatta?

19Due scuole si sfidano a tennis in partite soltanto di doppio. Ogni scuola è rappresentata da cinque studenti: vengono formate tutte le possibili coppie fra studenti della stessa scuola e ogni coppia di ciascuna scuola affronta una e una sola volta ogni coppia dell’altra. Quante partite deve giocare ognuno degli studenti?

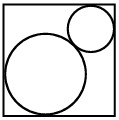
20Osserva la figura: due circonferenze hanno il centro sulla stessa diagonale di un quadrato, sono tangenti fra loro e tangenti internamente al quadrato. Il lato del quadrato è lungo 1 metro. Quanto vale la somma delle lunghezze, in metri, dei raggi delle due circonferenze?

21Chiama a e b le soluzioni dell’equazione x²- 3x + 1 = 0. Quanto vale a³ + b³ ?

22Il prodotto di tutti i divisori (interi) di 2007 vale

23La sequenza di lettere KANGAROOKANGAROO...KANGAROO è costruita scrivendo 20 volte di seguito la parola KANGAROO. Elimina dapprima tutte e sole le lettere che occupano nella sequenza un posto dispari; riaccosta quindi le lettere rimaste ed elimina ancora tutte e sole le lettere che nella nuova sequenza occupano un posto dispari; ripeti il procedimento fino a quando rimane una lettera sola. Che lettera è?

24In una città non ci sono due persone con lo stesso numero di capelli e nessuno ha esattamente 9999 capelli. Il numero degli abitanti della città è superiore al numero di capelli della persona che ne ha di più. Quanti possono essere al massimo gli abitanti di quella città?

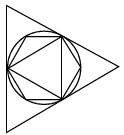
25Osserva la figura. Un triangolo equilatero di area t ed un esagono regolare di area E sono inscritti in una circonferenza, che a sua volta è inscritta in un altro triangolo equilatero di area T.Quale delle seguenti uguaglianze è vera?

26k è il più piccolo numero intero positivo con questa proprietà: 10k è un quadrato perfetto e 6k è un cubo perfetto. Quanti divisori (positivi) ha il numero k ?

27Da una cassaforte sono state rubate alcune collane di diamanti, tutte con lo stesso numero di diamanti (almeno 2 per collana). Tutti i diamanti che le componevano vengono ritrovati: il loro numero complessivo è compreso fra 200 e 300. L’investigatore che indaga sul furto, semplicemente contando i diamanti ritrovati, è in grado di risalire con certezza al numero delle collane rubate. Quante collane sono state rubate dalla cassaforte?

28Per ognuno di quattro colori diversi, in un’urna ci sono tre carte numerate da 1 a 3. Estrai a caso tre carte dall’urna. Quale fra i seguenti eventi è il più probabile?

29Ad una festa cinque amici si scambiano regali in modo che ciascuno faccia e riceva esattamente un regalo (e, naturalmente, che nessuno riceva il proprio regalo). In quanti modi diversi lo possono fare?

30In un tetraedro regolare la distanza fra due spigoli che non si tocchino è 6 centimetri. Qual è, in centimetri cubi, il volume del tetraedro?