1Qual è il risultato della divisione 20102010 : 2010?

2Carlo e Dario si sono sottoposti ad uno stesso test: Carlo ha totalizzato l’85% dei punti disponibili, Dario il 90%. In questo modo, Carlo ha totalizzato un punto in meno di Dario. Quanti erano i punti disponibili?

3Che numero devi sostituire al simbolo * se vuoi che la somma dei numeri presenti nella prima riga sia uguale a quella dei numeri presenti nella seconda?

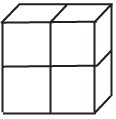
4Il solido in figura è ottenuto accostando quattro cubi identici: la superficie di ciascuno di essi misura 24 cm². Quanti centimetri quadrati misura la superficie del solido?

5Ad ogni compleanno, partendo dal primo, Ada ha ricevuto in regalo tanti fiori quanti erano gli anni che compiva. Ada li ha seccati e li ha conservati tutti: ora ne ha 120. Quanti anni ha oggi?

6Le due rive dell’Adige, nel tratto in cui attraversa Verona, sono collegate da cinque famosi ponti. Giulietta, partendo dalla sua casa in Verona, li ha percorsi tutti, ciascuno almeno una volta, e poi è rientrata a casa. Così facendo ha attraversato l’Adige n volte. Quale fra i seguenti è un possibile valore di n?

7Tre martedì di un certo mese sono giorni con data pari. In che giorno della settimana cade il 21 di quel mese?

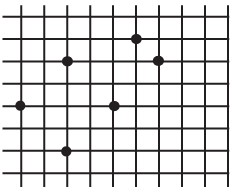
8La figura mostra sei punti marcati su un foglio di carta a quadretti (dove i quadretti hanno tutti la stessa dimensione). Quale fra le seguenti figure geometriche non può essere ottenuta congiungendo opportunamente alcuni di questi punti?

9La figura suggerisce come ottenere per via grafica l’uguaglianza 1 + 3 + 5 + 7 = 4 x 4. Con quale dei seguenti prodotti coincide la somma 1 + 3 + 5 + 7 + … + 27 + 29 + 31?

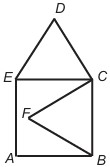
10Osserva la figura. ABCE è un quadrato, mentre BCF e CDE sono triangoli equilateri. Se AB ha lunghezza 1, quanto è lungo il segmento FD?

11Il prodotto fra l’età del mio professore e quella di suo padre è 2010. In che anno è nato il mio professore?

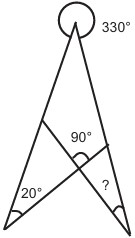
12In figura appaiono due triangoli ottusangoli parzialmente sovrapposti. Sono evidenziati quattro angoli: le misure (in gradi) di tre di essi sono quelle indicate. Quanti gradi misura il quarto angolo, indicato dal punto di domanda ? (Attenzione: nella figura non sono rispettate le proporzioni.)

13Per quanti numeri interi positivi accade che la somma delle cifre è 2010 e il prodotto delle cifre è 2 ?

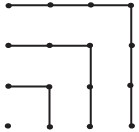
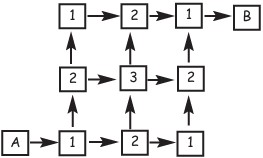
14Osserva la figura. Si vuole andare dal quadrato denotato con A a quello denotato con B rispettando i versi indicati dalle frecce. Per ogni possibile percorso di questo tipo vengono sommati i numeri inseriti nei quadrati attraversati. Quante somme diverse fra loro si possono ottenere?

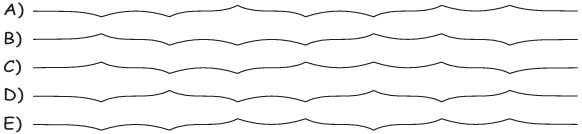
15Una lunga striscia di carta è stata piegata a metà tre volte, ogni volta senza riaprire la piegatura precedente; poi è stata riaperta e appoggiata su un tavolo: guardandola di profilo, si vedono ancora le 7 pieghe e i tratti della striscia tra essi compresi. L’aspetto della striscia di profilo può assomigliare solo a quattro delle linee disegnate sotto: quale è quella da scartare?

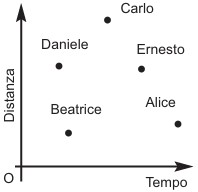
16I cinque ragazzi nominati in figura hanno fatto una corsa di allenamento. Sull’asse delle ascisse figura il tempo impiegato, su quello delle ordinate la distanza percorsa e la posizione dei singoli punti indica la prestazione del ragazzo corrispondente. Chi ha corso alla velocità maggiore?

17Osserva la figura: un cerchio di raggio 4 è suddiviso in quattro parti congruenti mediante l’impiego di archi di circonferenza di raggio 2. Quanto vale il perimetro di ciascuna di queste quattro parti?

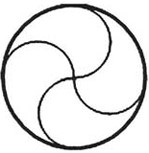
18Osserva la figura: un triangolo viene ripiegato su se stesso lungo il segmento tratteggiato in modo da ottenere la figura a destra. L’area del triangolo è una volta e mezza l’area della figura risultante e l’area della regione ombreggiata vale 1. Quanto vale l’area del triangolo originale?

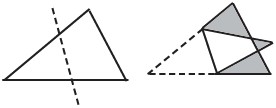
19In un supermercato vi sono due file di carrelli tutti uguali fra loro formate nel modo usuale, cioè infilando un carrello in quello che lo precede. Una fila è formata da 10 carrelli ed è lunga 2,9 metri, l’altra da 20 carrelli ed è lunga 4,9 metri. Quanto è lungo un carrello?

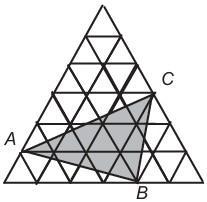
20Osserva la figura. Il triangolo grande è costruito accostando 36 triangoli equilateri, ciascuno di area 1. Quanto vale l’area del triangolo ABC ?

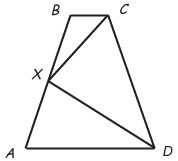
21Nel trapezio isoscele ABCD in figura, X è il punto medio del lato AB, la lunghezza di BX è 1 e l’angolo CXD è retto. Quanto vale il perimetro del trapezio ABCD ?

22Due lati del triangolo grande in figura sono suddivisi ciascuno in 10 segmenti uguali, che determinano le strisce evidenziate. Quale percentuale dell’area del triangolo risulta ombreggiata ?

23Per quanti numeri interi n compresi fra 1 e 100, estremi inclusi, il numero nⁿ è un quadrato perfetto?

24In una città vivono solo gentiluomini e bugiardi. Ogni singola affermazione pronunciata da un gentiluomo è vera, mentre ogni singola affermazione pronunciata da un bugiardo è falsa. Alcuni abitanti sono riuniti in una stanza e tre di loro fanno, una per ciascuno, le seguenti coppie di affermazioni: 1.“Non ci sono più di tre persone in questa stanza.” “Tutti noi mentiamo.” 2.“Non ci sono più di quattro persone in questa stanza.” “Non siamo tutti bugiardi.” 3.“Ci sono cinque persone in questa stanza.” “Tre di noi sono bugiardi.” Quante persone ci sono nella stanza e quanti bugiardi ci sono tra di loro?

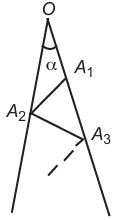
25L’angolo α rappresentato in figura misura 7 gradi; i punti A₁, A₃, … (indice dispari) sono presi in sequenza su un lato dell’angolo, mentre i punti A₂, A₄, … (indice pari) sono presi in sequenza sull’altro lato in modo che i segmenti OA₁, A₁A₂, A₂A₃, … siano tutti distinti, ma di uguale lunghezza. Una volta fissata tale lunghezza, il valore di n per cui il punto An ha la massima distanza possibile da O

26Una successione di numeri interi relativi è costruita come segue. I primi tre elementi sono, nell’ordine, 1, 2 e 3. Dal quarto in poi, ogni elemento è costruito sulla base degli ultimi tre che lo precedono, sottraendo l’ultimo ottenuto dalla somma del penultimo e del terzultimo: la successione inizia dunque con 1, 2, 3, 0, 5, -2, 7, … . Qual è l’elemento di posto 2010?

27In ogni vertice di un pentagono è scritto uno e un solo numero intero positivo. Si sa che due numeri posti in vertici adiacenti sono sempre primi fra loro (cioè non hanno divisori comuni diversi da 1) e che due numeri posti in vertici non adiacenti non lo sono mai. Vi sono diverse possibilità di realizzare questa situazione, ma uno e uno solo dei numeri seguenti non potrà mai comparire in alcun vertice. Quale?

28Quanti numeri interi positivi di tre cifre (significative) sono tali che la cifra centrale sia la media aritmetica delle altre due?

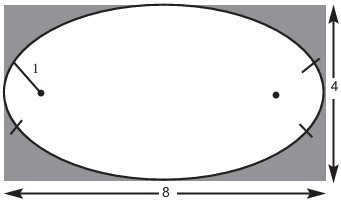
29La figura mostra un “ovale”, cioè una regione piana delimitata da quattro archi di circonferenza evidenziati dalle tacche che sezionano il suo contorno. In ciascuno dei quattro punti dove due diversi archi si saldano, i due archi hanno la stessa retta tangente. L’arco di sinistra ha misure identiche a quello di destra e l’arco inferiore ha misure identiche a quello superiore, sicché l’ovale presenta un asse di simmetria verticale e uno orizzontale. Il più piccolo dei raggi degli archi vale 1 e l’ovale si inserisce esattamente in un rettangolo di dimensioni 4 × 8. Quanto vale il più grande dei raggi?

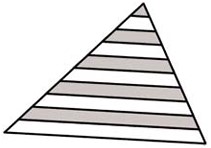
30Un codice a barre del tipo mostrato in figura è composto di strisce bianche e nere alternate, con la striscia iniziale e quella finale sempre nera. Ogni striscia è di ampiezza 1 o 2 e l’ampiezza totale è 12. Quanti differenti codici si possono costruire? (Ogni codice va letto da sinistra verso destra.)