1Quale dei seguenti numeri è il più grande?

2Osserva la figura: ai quadratini colorati in grigio puoi aggiungerne altri, senza che il perimetro della regione colorata in grigio aumenti. Quanti puoi aggiungerne, al massimo?

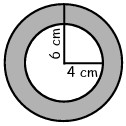
3Stefania ha due pendagli costruiti con lo stesso materiale, dello stesso spessore e dello stesso peso. Trascurando lo spessore, uno ha la forma di una corona circolare con raggio esterno di 6 cm e raggio interno di 4 cm, l'altro ha semplicemente la forma di un cerchio. Qual è il suo raggio in centimetri?

4a, b, c, d, e sono cinque numeri in progressione aritmetica. Si sa che b = 5.5 ed e = 10. Quanto vale a?

5Se 4ᵃ = 9 e 9ᵇ = 256, allora ab è uguale a

6Ognuna delle quattro carte che vedi in figura presenta su una faccia una lettera e sulla faccia opposta un numero. Pietro afferma: ”Qualunque sia la carta, se su una faccia c'è una vocale, sulla faccia opposta c'è un numero pari“. Alice non si fida e vorrebbe controllare. Quali carte è necessario e sufficiente che Alice rovesci per stabilire se Pietro ha detto la verità?

7In occasione di una partita particolarmente importante, il prezzo del biglietto per entrare allo stadio è stato aumentato del 20% rispetto alle partite precedenti. In conseguenza di questo, però, l'affluenza degli spettatori è diminuita del 20%. Rispetto alle partite precedenti l'incasso è

8Due circonferenze giacciono su uno stesso piano; i loro raggi misurano 3 metri e 5 metri e vi sono esattamente tre rette tangenti ad entrambe. Allora la distanza in metri fra i loro centri è

9Una mela, o una sua parte, che galleggino sulla superficie di un lago emergono da essa per 1/3 della loro massa. Un pesce e un gabbiano si gettano contemporaneamente su una mela intera che galleggia ed iniziano a mangiare rispettivamente la parte sommersa e la parte emergente. A parità di tempo impiegato, il gabbiano mangia il doppio del pesce. Quando tutta la mela sarà stata mangiata, quale frazione della mela avrà mangiato il gabbiano?

10Una galleria ha una sezione semi-circolare del diametro di 10 metri. Il tetto (piatto) di un autobus viene a contatto con la volta della galleria se le sue ruote di destra (a filo con la fiancata) sono a due metri dal bordo destro della galleria. Qual è in metri l'altezza dell'autobus?

11Se dividi 1001 per un opportuno numero di una cifra, ottieni per resto 5. Se dividi 2006 per lo stesso numero, che resto ottieni?

12Di tre numeri interi positivi a, b, c si sa che sono primi, che a > b > c, che a + b + c = 90 e che a - b - c = 28 . Quanto vale abc ?

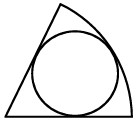
13Il raggio del settore circolare e il raggio del cerchio in figura stanno nel rapporto 3:1. In che rapporto stanno l'area del settore e l'area del cerchio?

14L'anno scorso in un coro polifonico gli uomini erano 30 in più rispetto alle donne. Quest'anno il numero degli elementi del coro è cresciuto del 10%: il numero delle donne è cresciuto del 20%, quello degli uomini del 5%. Quanti elementi ha il coro quest'anno?

15Considera tutti i numeri interi positivi di 9 cifre che puoi costruire usando per ciascuno tutte le 9 cifre 1,2,…,9. Supponi che ognuno di quei numeri sia scritto su un foglietto (un solo numero su ogni foglietto) e che i foglietti siano depositati in un'urna. Qual è il minimo numero di foglietti che ti basta estrarre dall'urna, se vuoi essere sicuro a priori che, fra i numeri riportati sui foglietti estratti, ve ne siano almeno due che, in qualche posizione, hanno la stessa cifra?

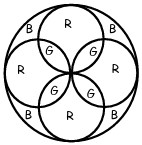
16Una finestra di una catterale presenta una vetrata come quella in figura, dove le lettere R, G e B rappresentano vetri di colore rispettivamente rosso, giallo e blu. La superficie occupata da vetro giallo misura 400 dm² . Quanti dm² misura la superficie occupata da vetro blu?

17Se a e b sono due numeri maggiori di 1, quale fra i numeri seguenti è il maggiore?

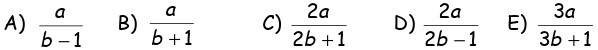
18Sedici squadre giocano un torneo di pallavolo. Ogni squadra affronta una e una sola volta ogni altra squadra: ad ogni partita, la squadra vincente avanza di un punto in classifica, mentre la squadra perdente rimane con il punteggio che aveva (non vi possono essere pareggi). Al termine del torneo, la classifica appare in progressione aritmetica. Quanti punti ha ottenuto la squadra che è arrivata ultima?

19Quanti angoli di ampiezza inferiore a 60° può avere, al massimo, un poligono convesso?

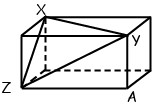
20In figura è rappresentato un parallelepipedo rettangolo. Le misure, in centimetri, dei lati del triangolo XYZ sono 8, 9 e √55. Quanto misura, in centimetri, la diagonale XA?

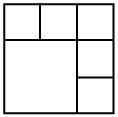
21In figura 1 appare una griglia 4×4 a celle bianche e grigie. Su di essa siamo autorizzati a compiere esclusivamente mosse del tipo seguente: scambiare fra loro due celle che stiano su una stessa riga o su una stessa colonna. Qual è il minimo numero di mosse che ci consente di ottenere la raffigurazione mostrata nella figura 2?

22Per quanti numeri interi positivi n la potenza n³⁰⁰ è un numero che, in notazione decimale, non ha più di 100 cifre?

23Quanti sottoinsiemi dell'insieme {1, 2, 3, …, 12} sono tali che la somma del più piccolo e del più grande dei loro elementi sia 13?

24Devo comporre un test formato da 10 quesiti, la risposta a ciascuno dei quali sia “sì” oppure “no”. Occorre strutturarlo in modo tale che chi lo affronta rispondendo “sì” a metà dei quesiti e “no” all'altra metà, fornisca comunque risposta corretta ad almeno 4 quesiti. Quante possibili liste di risposte corrette mi danno questa garanzia?

25Da una sequenza di dieci numeri interi consecutivi ne è stato rimosso uno. La somma dei nove numeri rimanenti è 2006. Qual è il numero rimosso?

26Voglio scrivere i numeri 1, 2, 3, 4, 5, 6 all'interno dei quadrati che compongono la figura (uno per ogni quadrato) in modo che, se due quadrati sono adiacenti, la differenza (positiva) dei numeri scritti in essi non sia 3. In quanti diversi modi lo posso fare? (Quadrati che abbiano in comune solo un vertice non vengono considerati adiacenti.)

27I numeri naturali sono stati raggruppati e sommati all'interno di ogni gruppo secondo il criterio suggerito qui di seguito 1, 2+3, 4+5+6, 7+8+9+10, 11+12+13+14+15, … Qual è la somma dei numeri ospitati nel centesimo gruppo?

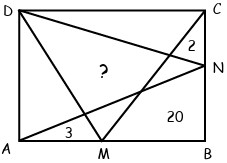
28Osserva la figura: ABCD è un rettangolo, M e N sono punti scelti a caso, rispettivamente, all'interno del lato AB e del lato BC. Il rettangolo risulta suddiviso in otto regioni per alcune delle quali è indicata l'area. Qual è l'area della regione quadrangolare indicata con “?” ?

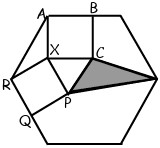
29In figura vedi un esagono di lato √3; XABC e XPQR sono quadrati. Quanto vale l'area del triangolo ombreggiato?

30Su una circonferenza sono stati scelti 8 punti in modo da massimizzare il numero dei punti distinti che siano intersezione di almeno due delle corde da essi individuate. Quanti sono i punti di intersezione (esclusi gli 8 punti scelti)?