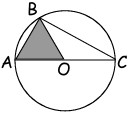
1Nella figura, O è il centro del cerchio e l’area della zona ombreggiata è √3. Qual è l’area del triangolo ABC?

2Secondo alcuni storici, gli antichi Egizi usavano una corda con due nodi per costruire un angolo retto. Se la lunghezza della corda è di 12 metri e uno dei nodi è al punto X, che dista 3 metri da uno dei capi della corda, a quanti metri dall’altro capo deve essere fatto il secondo nodo per avere un angolo retto in X?

3Ad un esame di ammissione all’Università, uno studente deve rispondere correttamente ad almeno l’80% delle domande di un questionario. Per adesso, Pietro ha esaminato 15 domande: non ha risposto a 5 di esse, ma è sicuro di aver risposto esattamente alle altre 10. Se risponde correttamente a tutte le domande rimanenti, raggiungerà esattamente l’80% di risposte giuste. Quante sono le domande nel questionario?

4Quanti divisori distinti ha 10ⁿ, se si contano anche 1 e 10ⁿ stesso?

5Scelti a caso tre dei vertici di un poligono regolare di 41 lati, qual è la probabilità che il triangolo da essi individuato risulti rettangolo?

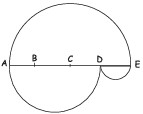
6Il segmento AE è diviso in 4 parti uguali dai punti ordinati B, C e D. Si disegna al di sopra del segmento AE una semicirconferenza di diametro AE mentre al di sotto del medesimo segmento si disegnano due semicirconferenze di diametro rispettivamente AD e DE (v. figura). Considera il percorso da A ad E lungo la semicirconferenza superiore e quello lungo l’unione delle due semicirconferenze inferiori: qual è il rapporto tra le lunghezze dei due percorsi, presi nell’ordine?

7Un cono e un cilindro circolari, entrambi di altezza h e con le basi di raggio r, sono in posizione tale che il volume della parte del cono contenuta nel cilindro è esattamente metà del volume del cono. Che frazione del volume del cilindro fornisce il volume della parte del cilindro contenuta nel cono?

8Delle quattro pareti che delimitano un cunicolo, le due laterali (opposte) sono verticali mentre pavimento e soffitto sono paralleli fra loro, ma non perpendicolari alle pareti laterali: di conseguenza la sezione verticale non è un rettangolo, ma un parallelogramma che, osservato dall’ingresso, presenta la parte più bassa sulla destra. A metà del cunicolo si vuole costruire una porta di sbarramento che sia costituita da due sezioni, superiore e inferiore, apribili l’una indipendentemente dall’altra. Guardando dall’ingresso, come vanno incernierate le due sezioni?

9Quanti numeri interi positivi di due cifre significative hanno la seguente proprietà: il quadrato della somma delle cifre è uguale alla somma dei quadrati delle cifre?

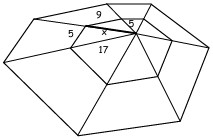
10Osserva la figura: un ragno con competenze matematiche ha tessuto una ragnatela formata da segmenti rettilinei, le cui lunghezze sono tutte numeri interi. Quanto vale x?

11Tommaso è nato il giorno in cui sua mamma compiva 20 anni e così festeggiano il compleanno insieme. Se vivono entrambi sufficientemente a lungo, quante volte l’età (in anni) di Tommaso sarà un divisore dell’età di sua mamma?

12Assegnato un quadrato ABCD di lato 1 si considerino tutti i quadrati che hanno in comune con ABCD almeno due vertici. L’area della regione del piano formata dai punti che appartengono ad almeno uno di tali quadrati è

13La misura dell’angolo β è il 25% in meno della misura dell’angolo γ e il 50% in più della misura dell’angolo α. Ne deduciamo che la misura dell’angolo γ è

14Assegnata l’equazione, vedi la figura, dove x e y sono interi, il valore x della soluzione (x, y) è

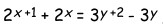
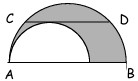
15Si considerino due semicerchi disegnati come in figura. La corda CD, di lunghezza 4, è parallela al diametro AB del semicerchio più grande ed è tangente al semicerchio più piccolo. L’area della regione di piano ombreggiata in figura è

16La somma di cinque interi consecutivi è uguale a quella dei tre interi consecutivi immediatamente seguenti. Qual è il più grande di questi otto numeri?

17Un’isola è abitata solo da cavalieri e mentitori. Tutti i cavalieri dicono sempre il vero e tutti i mentitori dicono sempre il falso. Un abitante dell’isola, che indicheremo con A, alla domanda se lui e un altro abitante dell’isola, detto B, siano cavalieri o mentitori, risponde che almeno uno dei due è un mentitore. Quale delle seguenti affermazioni è vera?

18Si consideri una sfera di raggio 3 con centro nell’origine di un sistema ortogonale di tre assi cartesiani. Quanti punti ci sono sulla superficie della sfera che hanno tutte le coordinate intere?

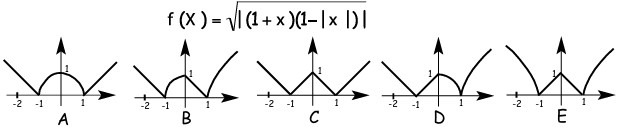
19Quale dei seguenti è il grafico della funzione f definita da

20Marco e Giorgio vanno in piscina; si tuffano insieme e ciascuno dei due nuota a velocità costante. Al termine della ottava vasca Marco raggiunge per la prima volta Giorgio e lo supera; se smettono di nuotare contemporaneamente, ma alle due estremità opposte della piscina, quale dei seguenti può essere il numero di vasche che ha percorso Marco?

21Se f(x) come in figura e f(g(x)) = x, allora g(x)=

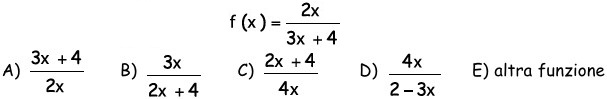
22Quale dei seguenti numeri non può essere scritto come x + √x con x intero?

23Qual è il massimo valore che può assumere il rapporto tra un numero di tre cifre e la somma delle sue cifre?

24Quanti sono gli a reali tali che l’equazione quadratica x² + ax + 2007 = 0 abbia due soluzioni intere?

25Ad una festa cinque amici si scambiano regali in modo che ciascuno faccia e riceva esattamente un regalo (e, naturalmente, che nessuno riceva il proprio regalo). In quanti modi diversi lo possono fare?

26La somma in figura è uguale a

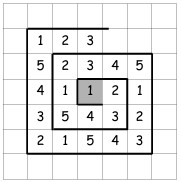
27Le cifre della successione 1234512345123451 … riempiono le celle su un foglio con una legge del tipo a spirale, partendo dalla cella segnata (v. figura). Quale cifra si viene a trovare sulla cella che sta esattamente 100 celle sopra quella ombreggiata?

28Un intero positivo di 5 cifre viene detto “numero dispettoso” se non può essere espresso come prodotto di due interi di 3 cifre ciascuno. Quanto può essere lunga al massimo una sequenza di numeri consecutivi che siano tutti dispettosi?

29La successione 1, 3, 4, 9, 10, 12, 13, … è costituita da tutti e soli i numeri che sono potenze di 3 o che possono essere scritti come somma di potenze di 3 diverse tra loro, messi in ordine crescente. Qual è il centesimo elemento della successione?

30Anna, Linda e Carlo giocano lanciando un unico dado. Anna vince se ottiene 1, 2 o 3, Linda se ottiene 4 o 5 e Carlo solo se ottiene 6. Il turno ruota da Anna a Linda a Carlo e di nuovo ad Anna, ecc., finché uno dei giocatori vince. La probabilità che Carlo vinca è