1Nelle celle di un tabella 2 x 2 sono scritti (uno per cella) i numeri 3 e 4 e due numeri non noti. Si sa che la somma dei numeri di una riga è 5, la somma dei numeri dell’altra riga è 10 e la somma dei numeri di una colonna è 9. Qual è il più grande dei due numeri incogniti?

2Se x + y = 0 e x ≠ y, allora

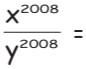
3In una tabella rettangolare 33 x 21 le righe sono numerate da 1 a 33 e le colonne sono numerate da 1 a 21. Cancelliamo le righe il cui numero non è un multiplo di 3 e le colonne il cui numero è pari. Quante celle rimangono nella tabella?

4Quanti numeri primi p hanno la proprietà che anche p⁴ + 1 è primo? (Ricorda che 1 non è un numero primo.)

5Un fiume inizia nel punto A. Nel suo corso si divide in due; il primo ramo riceve i 2/3 dell’ acqua e il secondo il resto. Più avanti il primo ramo si divide in tre sottorami, di cui il primo riceve 1/8 dell’ acqua, il secondo 5/8 e il terzo il resto. Infine quest’ultimo sottoramo incontra il secondo ramo della prima biforcazione del fiume: la mappa qui sotto illustra la situazione. Che parte dell’acqua iniziale fluisce nel punto B?

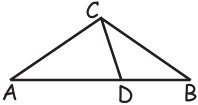
6È dato un triangolo isoscele ABC (CA = CB). Il punto D sul lato AB è tale che AD = AC e DB = DC (vedi figura). Allora la misura dell’angolo ACB è

7Una scatola contiene sette carte numerate da 1 a 7. Due saggi pescano a caso delle carte dalla scatola: il primo ne prende tre, il secondo due delle rimanenti; le ultime due restano chiuse nella scatola. Il primo saggio, dopo aver guardato solo i numeri scritti sulle carte da lui pescate, dice al secondo: “Sono certo che la somma dei numeri riportati sulle tue carte è pari”. Quanto vale la somma dei numeri riportati sulle carte pescate dal primo saggio?

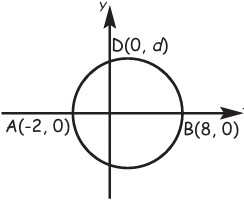
8Nel cerchio disegnato in figura, AB è un diametro. Determina l’ordinata d del punto D.

9Sappiamo che x²yz³=7³ e xy²=7⁹. Allora xyz=

10Vuoi sistemare in ogni posto vuoto dell’allineamento 2_ _8 una cifra in modo da ottenere un numero di quattro cifre divisibile per 3. Quante scelte hai per la coppia (ordinata) di cifre da inserire?

11Hai i seguenti sette numeri: –9; 0; –5; 5; –4; –1; –3. Utilizzando sei di essi vuoi formare tre coppie in modo tale che la somma dei numeri di ogni coppia sia sempre la stessa. Che numero devi escludere?

12La lunghezza dello spigolo di ciascuno dei cubi in figura è 1. Qual è la lunghezza del segmento AB?

13Ad una gara matematica vengono proposti cinque problemi. I punteggi attribuiti ad essi sono tutti diversi tra loro e sono tutti interi positivi. Roberto ha risolto tutti i cinque problemi correttamente, ottenendo 10 punti in totale per i due problemi con i punteggi minori e 18 punti in totale per i due problemi con i punteggi maggiori. Quanti punti ha ottenuto Roberto in totale per i cinque problemi?

14Matilde ha disegnato 36 canguri usando tre colori distinti. Il bianco è stato usato per 25 canguri, il rosso per 28 e il nero per 20. Solo per 5 canguri sono stati usati tutti e tre i colori. Quanti dei canguri disegnati sono di un solo colore?

15Osserva la figura. Tre circonferenze di raggio 1 sono a due a due tangenti esternamente. Quanto vale l’area della regione ombreggiata?

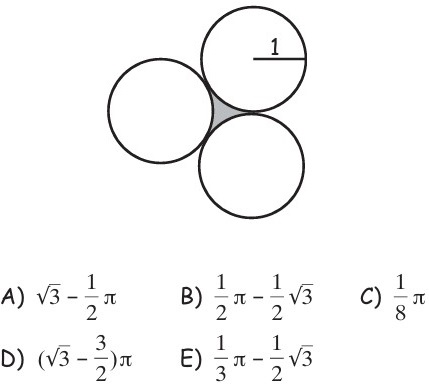
16Le lunghezze degli spigoli di un parallelepipedo rettangolo, misurata in centimetri, sono numeri interi e formano una progressione geometrica di ragione q = 2. Quale delle seguenti misure, in centimetri cubi, può rappresentare il volume del solido?

17Il numeratore e il denominatore di una frazione sono numeri negativi e il numeratore è maggiore di uno del denominatore. Quale delle seguenti affermazioni è vera?

18Cinque punti distinti A₁, A₂, A₃, A₄ e A₅, sono disposti nell’ordine su una retta. Viene scelto un punto P sulla stessa retta in modo che la somma delle distanze PA₁ + PA₂ + PA₃ + PA₄ + PA₅ sia minima. Si può affermare che il punto P è

19Si scelgano a caso tre punti dalla griglia in figura. Qual è la probabilità che essi siano collineari?

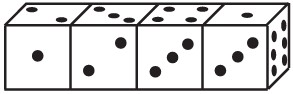
20Quattro dadi identici sono accostati come in figura. Le facce di ciascun dado sono numerate da 1 a 6, ma i dadi non sono standard, cioè la somma dei punti di due facce opposte non è necessariamente 7. Qual è la somma dei punti delle 6 facce ciascuna delle quali viene a contatto con qualche altra faccia?

21Una pedina posta al centro di una griglia quadrata 5 x 5 viene mossa con passi orizzontali o verticali di ampiezza uno, determinati dal lancio simultaneo di una coppia di dadi, uno rosso e uno blu. Il dado rosso fa muovere la pedina di un passo verso destra se esce un numero pari e verso sinistra se esce un numero dispari, il dado blu fa muovere la pedina di un passo verso l’alto se esce un numero pari e verso il basso se esce un numero dispari. Qual è la probabilità che dopo due lanci la pedina sia tornata al punto di partenza?

22Il numero 3³²– 1 ha esattamente due divisori (interi) entrambi maggiori di 75 e minori di 85. Quanto vale il prodotto di questi due divisori?

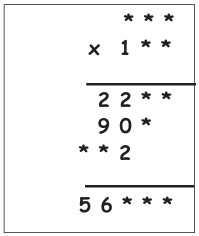
23La figura rappresenta una moltiplicazione eseguita manualmente nel modo usuale. Ogni asterisco sostituisce una cifra. La somma delle cifre del prodotto è

24È noto che x + y + z = 1 e 1/x + 1/y + 1/z = 0. Allora l’espressione x² + y² + z²

25Sia {aₙ} una successione. È noto che a₁ = 0 e che, per n ≥ 0, si ha aₙ₊₁ = aₙ + (-1)ⁿ × n. Se aₖ = 2008, allora il valore di k è

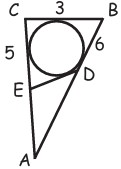
26Osserva la figura. Nel triangolo ABC è inscritto un cerchio. Si sa che |AC| = 5, |AB| = 6, |BC| = 3 e che il segmento ED è tangente al cerchio. Il perimetro del triangolo ADE vale

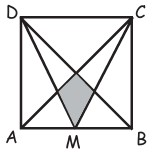
27Il quadrato ABCD ha il lato di lunghezza 1 e M è il punto medio di AB. L’area della regione ombreggiata vale

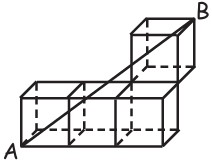
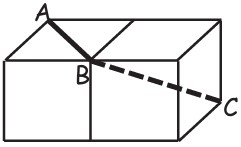
28I due cubi in figura hanno una faccia in comune. Qual è, in gradi, la misura dell’angolo ABC?

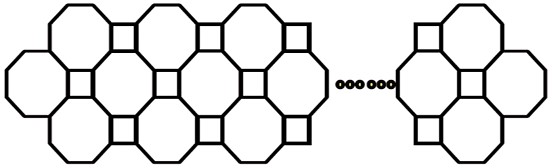
29Per costruire questa decorazione sono state usate (senza piegarle) sbarrette metalliche. Si sa che nella decorazione compaiono 61 ottagoni. Quante sbarrette sono state usate?

30Quanti sono i numeri interi positivi n di 2007 cifre (in rappresentazione decimale) con la seguente proprietà: ogni numero intero di due cifre costituito da due cifre consecutive di n (nello stesso ordine in cui compaiono in n) è divisibile per 17 o per 23?