1In un acquario ci sono 200 pesci: l’1% di essi è blu, mentre tutti gli altri sono gialli. Quanti pesci gialli dobbiamo togliere dall’acquario se vogliamo che i pesci blu siano il 2% di tutti i pesci rimasti?

2Qual è il più grande tra i seguenti numeri?

3Per quanti valori interi positivi di n il numero n² + n è un numero primo?

4Maria, Guglielmo e Oscar sono stati in pizzeria. Ciascuno di essi ha preso una pizza quattro stagioni, due lattine di birra e una fetta di torta. Naturalmente le pizze hanno tutte lo stesso prezzo, e così pure le lattine di birra e le fette di torta. Quale dei seguenti importi può essere il totale pagato dai tre amici?

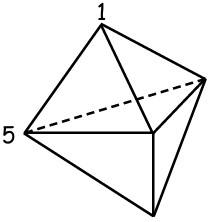
5Il solido in figura ha 6 facce, tutte triangolari. Ad ogni suo vertice viene associato un numero in modo che la somma dei numeri associati ai tre vertici di ogni singola faccia sia la stessa per tutte le facce. La figura indica i numeri associati a due dei vertici. Quanto vale la somma di tutti i numeri impiegati?

6Due circonferenze, una di centro F e raggio 13 e l’altra di centro G e raggio 15, si intersecano nei punti P e Q. Se la lunghezza della corda PQ è 24, quale è la lunghezza del segmento FG?

7Una scatola contiene 2 calze bianche, 3 calze rosse e 4 calze blu. Lisa sa che un terzo delle calze sono bucate, ma non sa di quale colore siano. Prende a caso le calze dalla scatola: quante deve prenderne per essere sicura di avere almeno un paio di calze non bucate e dello stesso colore?

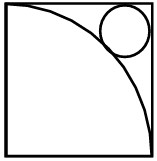
8La circonferenza disegnata nel quadrato in figura è esternamente tangente a un quarto di circonferenza di raggio 1 e a due lati del quadrato. Qual è il suo raggio?

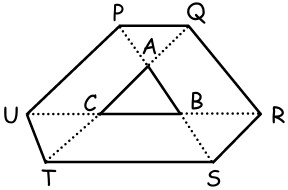
9I lati del triangolo ABC vengono prolungati ciascuno da entrambe le parti, generando punti P, Q, R, S, T e U tali che | PA| = |AB| = |BS|, |TC| = |CA| = |AQ| e |UC | = |CB | = |BR|. Se l’area di ABC è 1, qual è l’area dell’ esagono PQRSTU?

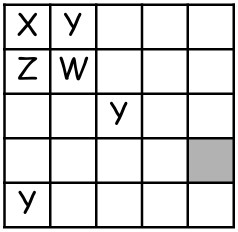
10Vogliamo colorare le celle della griglia in figura usando i quattro colori diversi X, Y, Z, W in modo che due celle che sono a contatto non ricevano mai lo stesso colore (due celle si considerano a contatto se hanno in comune almeno un vertice). La figura mostra che alcuni colori sono già stati assegnati. Con quali colori può essere colorata la cella ombreggiata?

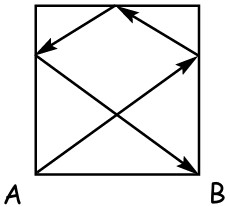
11Su un tavolo da biliardo, quadrato e con lato 2, viene lanciata una palla dall’angolo A. La palla tocca tre lati come mostrato in figura, e termina la sua corsa nell’angolo B. Quanto è lungo il percorso compiuto dalla palla? (Si ricorda che l’angolo di incidenza ha la stessa ampiezza dell’angolo di riflessione.)

122009 canguri, alcuni col pelo chiaro e altri con il pelo scuro, hanno misurato le loro altezze. Ci sono: un canguro chiaro che è più alto di esattamente 8 canguri scuri, un canguro chiaro che è più alto di esattamente 9 canguri scuri, un canguro chiaro che è più alto di esattamente 10 canguri scuri, e così via, e uno e un solo canguro chiaro è più alto di tutti i canguri scuri. Quanti sono i canguri chiari?

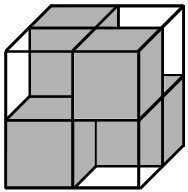
13Un cubo il cui spigolo misura 2 è costituito da 8 cubetti di spigolo 1, quattro trasparenti e quattro non trasparenti, disposti in modo che non sia possibile vedere attraverso il cubo, né dal lato frontale, né da sopra a sotto né da destra a sinistra (v.figura). Vogliamo costruire un cubo di spigolo 3 accostando sempre cubetti di spigolo 1 e in modo che, esattamente come sopra, non sia possibile vedere attraverso il cubo. Qual è il numero minimo di cubetti non trasparenti che ci consente di riuscirci?

14Su un’isola vivono due categorie di persone: i sinceri, che non mentono mai, e i bugiardi, che mentono sempre. Su quest’isola ci sono 25 persone in fila. Ognuno, tranne il primo della fila, dice che la persona davanti a lui nella fila è un bugiardo mentre il primo dice che tutti quelli dietro di lui sono bugiardi. Quanti bugiardi ci sono nella fila?

15Qual è l’ultima cifra del numero 1² − 2² + … − 2008² + 2009² ?

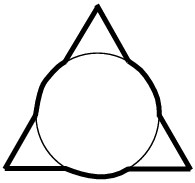
16Sovrapponiamo un triangolo equilatero con il lato lungo 3 ad un cerchio di raggio 1 in modo che i centri delle due figure coincidano (v. figura). Quanto è lungo il perimetro della figura che otteniamo?

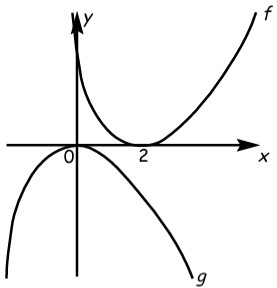
17f e g sono due funzioni reali di variabile reale, tali che i loro grafici (sottoinsiemi di R2) possano essere sovrapposti mediante un opportuno movimento rigido in R3. La figura mostra la loro posizione relativa. Qual è la relazione tra f e g ?

18A ciascuno dei 100 partecipanti ad una gara di Matematica sono stati proposti 4 problemi. 90 ragazzi hanno risolto il primo problema correttamente, 85 il secondo, 80 il terzo e 70 il quarto. Qual è il più grande valore di n per il quale posso affermare con certezza che almeno n ragazzi hanno risolto correttamente tutti e quattro i problemi?

19Nelle prime due figure, per un solido geometrico sono schematizzate l’immagine frontale (il segmento verticale centrale indica uno spigolo) e l’immagine dall’alto. Quale delle altre figure può essere la visione schematizzata del solido dal lato sinistro?

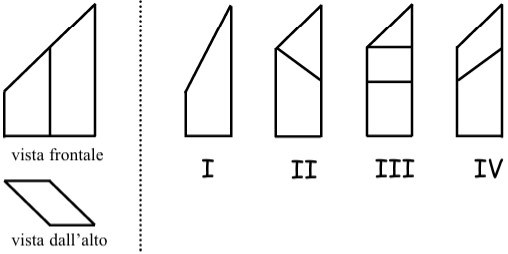
20Quanti sono i numeri di dieci cifre contenenti solo le cifre 1, 2 e 3 nei quali due qualsiasi cifre adiacenti differiscono di 1?

21Sia N il numero dei numeri di 8 cifre che hanno tutte le cifre non nulle e diverse tra loro. Quanti sono i numeri di 8 cifre che hanno tutte le cifre non nulle, diverse tra loro, e che sono divisibili per 9?

22Due podisti, A e B, corrono, ciascuno a velocità costante, lungo una pista circolare. A corre più veloce di B ed impiega 3 minuti per fare un giro completo della pista. A e B partono insieme e dopo 8 minuti A raggiunge B per la prima volta. Quanto impiega B a fare un giro completo della pista?

23Dobbiamo costruire una tabella 3 x 3 di numeri reali in cui la somma degli elementi sia la stessa per righe, per colonne e per diagonali. Due dei numeri ci sono stati imposti e sono collocati come in figura. Che numero dobbiamo collocare nella posizione a?

24Quanti sono gli interi n ≥ 3 per i quali esiste un poligono convesso di n lati tale che i suoi angoli siano proporzionali ai numeri 1, 2, …, n?

2555 alunni partecipano ad un gara di Matematica che consiste nel rispondere ad alcuni quesiti. La valutazione degli elaborati viene fatta redigendo una stringa di “+”, “-“ e “0”, che stanno ad indicare rispettivamente risposta corretta, risposta errata, nessuna risposta. Alla fine della valutazione risulta che non ci sono due stringhe con lo stesso numero di “+” e di “-“ . Qual è il numero minimo di quesiti che deve essere stato assegnato perché questo possa accadere?

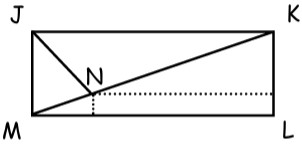
26In un rettangolo JKLM, la bisettrice dell’angolo KJM interseca la diagonale KM nel punto N. Le distanze di N dai lati LM e KL sono rispettivamente 1 ed 8. Qual è la lunghezza di LM ?

27Per quanti diversi valori del parametro reale k il sistema di equazioni in x, y, z ammette soluzione?

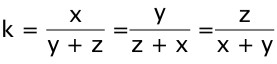
28I numeri 1, 2, …, 99 sono distribuiti in ngruppi in modo da soddisfare le condizioni seguenti: 1.ogni numero sta in uno e in un solo gruppo; 2.ogni gruppo contiene almeno due numeri; 3.se due numeri stanno nello stesso gruppo, la loro somma non è divisibile per 3. Qual è il minimo valore possibile per n?

29Isabella e le sue tre sorelle vanno a teatro. Ciascuna di esse ha prenotato uno dei 4 posti di un palco. Isabella e due delle sorelle arrivano in anticipo ed occupano a caso tre dei quattro posti. Quando arriva la quarta sorella, Maria, pretende di occupare il posto che era stato prenotato a nome suo: se non è quello libero, anche la sorella che lo deve liberare ha la stessa pretesa. Che probabilità c’è che Isabella debba cambiare posto?

30Definiamo, per ricorrenza, la successione di interi {aₙ} nel modo seguente: a₀= 1, a₁= 2, …, aₙ₊₂= aₙ+ (aₙ₊₁)². Il resto della divisione di a₂₀₀₉ per 7 vale